题目内容
4.若等式x4+4x3+3x2+2x+1=(x+1)4+a(x+1)3+b(x+1)2+c(x+1)+d恒成立,则(a,b,c,d)等于( )| A. | (1,2,3,-1) | B. | (2,3,4,-1) | C. | (0,-1,2,-2) | D. | (0,-3,4,-1) |
分析 把等式的右边按照二项式定理展开,比较系数,求得a,b,c,d的值,可得结论.
解答 解:∵等式x4+4x3+3x2+2x+1=(x+1)4+a(x+1)3+b(x+1)2+c(x+1)+d恒成立,
又(x+1)4+a(x+1)3+b(x+1)2+c(x+1)+d
=(x4+4x3+6x2+4x+1)+a(x3+3x2+3x+1)+b(x2+2x+1)+c(x+1)+d
=x4+(4+a)x3+(6+3a+b)x2+(4+3a+2b+c)x+1+a+b+c+d,
∴4+a=4,6+3a+b=3,4+3a+2b+c=2,1+a+b+c+d=1,
求得a=0,b=-3,c=4,d=-1,则(a,b,c,d)=(-1,0,1,1),
故选:D.
点评 本题主要考查二项式定理的应用,属于中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.运行如图的程序框图,则输出s的值为( )
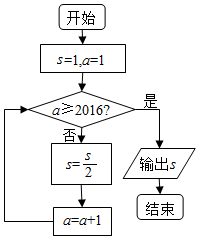

| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
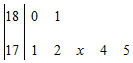 (文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.
(文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.