题目内容
8.如图是某算法的程序框图,若实数x∈(-1,4),则输出的数值不小于30的概率为$\frac{2}{5}$.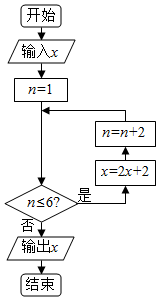
分析 由程序框图的流程,写出前三次循环得到的结果,得到输出的值与输入的值的关系,令输出值大于等于30得到输入值的范围,利用几何概型的概率公式求出输出的x不小于30的概率.
解答 解:设实数x∈(-1,4),
经过第一次循环得到x=2x+2,n=3,
经过第二循环得到x=2(2x+2)+2,n=5,
经过第三循环得到x=2[2(2x+2)+2]+2,n=7,
此时输出x,
输出的值为8x+14,
令8x+14≥30,得x≥2,
由几何概型得到输出的x不小于30的概率为P=$\frac{4-2}{4+1}$=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 解决程序框图中的循环结构时,一般采用先根据框图的流程写出前几次循环的结果,根据结果找规律,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
20.已知某程序框图如图所示,则执行该程序后输出的结果是( )


| A. | -1 | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
18.集合A={x|x2-2x-3<0},B={x||x|<2},则A∩B=( )
| A. | {x|-1<x<2} | B. | {x|1<x<3} | C. | {x|-2<x<1} | D. | {x|-2<x<2} |
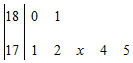 (文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.
(文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.