题目内容
15.求1,1+2,1+2+3,1+2+3+4,1+2+3+4+5,1+2+3+4+…+n,…的前n项和.分析 由等差数列求得1+2+3+4+…+n=$\frac{1}{2}$(n2+n),从而拆项求和即可.
解答 解:易知1+2+3+4+…+n
=$\frac{(n+1)n}{2}$=$\frac{{n}^{2}}{2}$+$\frac{n}{2}$=$\frac{1}{2}$(n2+n),
故1+(1+2)+(1+2+3)+(1+2+3+4)+(1+2+3+4+5)+…+(1+2+3+4+…+n)
=$\frac{1}{2}$(12+1)+$\frac{1}{2}$(22+2)+$\frac{1}{2}$(32+3)+$\frac{1}{2}$(42+4)+$\frac{1}{2}$(52+5)+…+$\frac{1}{2}$(n2+n)
=$\frac{1}{2}$[(12+22+32+…+n2)+(1+2+3+…+n)]
=$\frac{1}{2}$($\frac{n(n+1)(2n+1)}{6}$+$\frac{n(n+1)}{2}$)
=$\frac{1}{2}$•$\frac{n(n+1)(2n+4)}{6}$
=$\frac{n(n+1)(n+2)}{6}$.
点评 本题考查了等差数列的前n项和公式的应用及拆项求和法的应用.

练习册系列答案
相关题目
5.已知全集U=R,集合A={0,1,2,3,4},B={x|0<x<3},则如图中阴影部分所表示的集合为( )
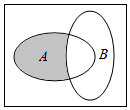

| A. | {0,1,2} | B. | {0,1,} | C. | {0,3,4} | D. | {3,4} |
6.下列函数为偶函数的是( )
| A. | f(x)=x2-x | B. | f(x)=xcosx | C. | f(x)=xsinx | D. | $f(x)=1g({x+\sqrt{{x^2}+1}})$ |
20.函数y=sin($\frac{π}{3}$-2x)+sin2x的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
7.从1、2、3、4、5这5个数中随机取出一个数,取出的数是某个整数的平方数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.等差数列-6,-1,4,9,…中的第20项为( )
| A. | 89 | B. | -101 | C. | 101 | D. | -89 |