Question

【题目】某营养学家建议：高中生每天的蛋白质摄入量控制在（单位：克），脂肪的摄入量控制在（单位：克），某学校食堂提供的伙食以食物和食物为主，1千克食物含蛋白质60克，含脂肪9克，售价20元；1千克食物含蛋白质30克，含脂肪27克，售价15元.

（1）如果某学生只吃食物，判断他的伙食是否符合营养学家的建议，并说明理由；

（2）为了花费最低且符合营养学家的建议，学生需要每天同时食用食物和食物各多少千克？并求出最低需要花费的钱数.

Answer 1

【答案】（1）见解析；（2）见解析

【解析】试题分析：（1）根据A满足蛋白质的摄入量时确定脂肪摄入量，A满足脂肪摄入量时确定蛋白质的摄入量，再对照专家标准进行比较判断（2）设学生每天吃千克食物， 千克食物，则目标函数为，再根据条件列约束条件，画出可行域，求目标函数最小值

试题解析：（1）解：如果学生只吃食物，则蛋白质的摄入量在（单位：克）时，食物的重量在（单位：千克），其相应的脂肪摄入量在（单位：克），不符合营养学家的建议；当脂肪的摄入量在（单位：克）时，食物的重量在（单位：千克），其相应的蛋白质摄入量在（单位：克），不符合营养学家的建议.

（2）设学生每天吃千克食物， 千克食物，每天的伙食费为，

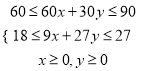由题意满足，即，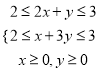

可行域如图所示，

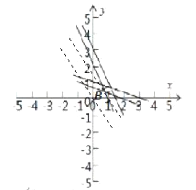
把变形为，得到斜率为，在轴上截距为的一族平行直线.由图可以看出，当直线经过可行域上的点时，截距最大.

解方程组，得点的坐标为，

所以元，

答：学生每天吃0.8千克食物，0.4千克食物，既能符合营养学家的建议又花费最少.最低需要花费22元.