Question

【题目】设点,,为坐标原点，点满足=+，（为实数）；

（1）当点在轴上时，求实数的值；

（2）四边形能否是平行四边形？若是,求实数的值；若不是，请说明理由．

Answer 1

【答案】（1）（2）四边形OABP不是平行四边形

【解析】

试题分析：（1）设点P（x，0），由=+得（x，0）=（2，2）+t（3，2 ），解出t值．（2），设点P（x，y），假设四边形OABP是平行四边形，根据向量平行得出坐标间的关系，由=+，推出矛盾，故假设是错误的

试题解析：（1）设点P（x，0）， =（3,2）,

∵=+，∴ （x,0）=（2,2）+t（3,2）,

∴

（2）设点P（x,y），假设四边形OABP是平行四边形，

则有∥, y=x―1, ∥ 2y=3x ……①,

又由=+， （x,y）=（2,2）+ t（3,2）,得 ∴ ……②,

由①代入②得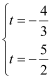：， 矛盾，∴假设是错误的，

∴四边形OABP不是平行四边形。