题目内容

9．命题p：关于x的方程x2+mx+m=0无实根，命题q：函数f（x）=（m+1）x在R上为减函数，若“p∨q”为假命题，求实数m的取值范围．

分析 分别求出命题p真、命题q真m的范围，由“p∨q”为假命题，得p、q”都为假命题，列式计算．

解答 解：命题p真时：△=m2-m＜0得0＜m＜4，命题q真时：0＜m+1＜2得-1＜m＜1，
若“p∨q”为假命题，则p、q”都为假命题，$\left\{\begin{array}{l}{m≤0或m≥4}\\{m≤-1或m≥1}\end{array}\right.$⇒m≤-1或m≥4，
∴实数m的取值范围：{m|m≤-1或m≥4}

点评 本题考查了命题真假的应用，属于基础题．

练习册系列答案
相关题目
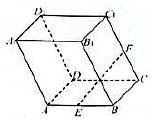19．如图所示，在平行六面体ABCD-A1B1C1D1中，底面是边长为2的正方形，侧棱AA1的长为2，且∠A1AB=∠A1AD=120°，E为AB的中点，F为CC1的中点，则EF的长为$\sqrt{3}$．
20．计算：$lg4+lg9+2\sqrt{{{（{lg6}）}^2}-lg36+1}$=2．
17．已知函数f（x）=sin（ωx+φ）-b（ω＞0，0＜φ＜π）的图象两相邻对称轴之间的距离是$\frac{π}{2}$，若将f（x）的图象先向右平移$\frac{π}{6}$个单位，再向上平移$\sqrt{3}$个单位，所得函数g（x）为奇函数．
（1）求f（x）的解析式；
（2）求f（x）的对称轴及单调区间．
4．设f0（x）=sinx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x），n∈N，则f2017（x）=（　　）
A．sinxB．-sinxC．cosxD．-cosx
14．（1）计算$\frac{1-i}{{{{（1+i）}^2}}}+\frac{1+i}{{{{（1-i）}^2}}}$
（2）求中心在原点，焦点在坐标轴上，并且经过点P（3，$\frac{15}{4}$）和Q（$\frac{16}{3}$，5）的双曲线方程．
1．设函数f（x）=axlnx+$\frac{1}{x}$（a＞0）．
（Ⅰ）当a=1时，讨论f（x）的单调性；
（Ⅱ）设g（x）=f（x）-ax，若g（x）≥0恒成立，求a的取值范围．
16．我市正在建设最具幸福感城市，原计划沿渭河修建7个河滩主题公园．为提升城市品位、升级公园功能，打算减少2个河滩主题公园，两端河滩主题公园不在调整计划之列，相邻的两个河滩主题公园不能同时被调整，则调整方案的种数为（　　）
A．12B．8C．6D．4
17．已知函数$f（x）=sin（{x+\frac{π}{2}}）cos（{x-\frac{π}{3}}）$．
（1）求函数f（x）的最小正周期；
（2）将函数y=f（x）的图象向下平移$\frac{1}{4}$个单位，再将图象上各点的纵坐标伸长为原来的4倍（横坐标不变），得到函数y=g（x）的图象，求函数y=g（x）在$[{0，\frac{π}{3}}]$上的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网