题目内容

15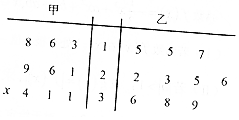．甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示，则“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

分析 x=9时计算甲乙的平均数，比较大小，然后已知甲运动员得分平均数大于乙运动员得分平均数得到x可能比9大，因此得到选项．

解答 解：由题意，x=9时甲的平均数为$\frac{18+16+13+29+26+21+31+31+34+39}{10}$=25.8；
乙的平均数为$\frac{15+15+17+22+23+25+26+36+38+39}{10}$=25.6＞25.8，
所以“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的充分条件；而已知甲运动员得分平均数大于乙运动员得分平均数得到x可能比9大，
因此已知甲运动员得分平均数大于乙运动员得分平均数的充分不必要条件；
故选：A．

点评 本题考查了由茎叶图计算平均数以及充分必要条件的判断；属于基础题．

练习册系列答案
相关题目
5．一个四棱锥的三视图在1×1的方格中显示如图，则此几何体的体积为（　　）
A．8B．4C．3D．$\frac{8}{3}$
6．如图，四边形ABCD中，∠CBD=α，∠C=β，∠A+β=π，AB=2，AD=1，$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ
（1）求角β的大小
（2）求四边形ABCD周长的取值范围．
3．已知函数f（x）=$\left\{{\begin{array}{l}{x+2，x＞a}\\{{x^2}+5x+2，x≤a}\end{array}}$，若函数g（x）=f（x）-2x恰有三个不同的零点，则实数a的取值范围是（　　）
A．[-1，1）B．[-1，2）C．[-2，2）D．[0，2]
10．设函数y=f（x）在区间[0，1]上的图象是连续不断的一条曲线，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算由曲线y=f（x）及直线x=0，x=1，y=0所围成部分的面积S，先生产两组（每组N个）区间[0，1]上均匀随机数x1，x2，…，xN和y1，y2，…，yN，由此得到N个点（xi，yi）（i=1，2，…，N），再数出其中满足yi≤f（xi）（i=1，2，…，N）的点数N1，那么由随机模拟方法可得S的近似值为$\frac{{N}_{1}}{N}$．
20．已知一个几何体的三视图如图所示（单位：m），其中俯视图为正三角形，则该几何体的体积为$\frac{4\sqrt{3}}{3}$m3．
7．在（3x2-$\frac{1}{x}$）6的二项展开式中，x3项的系数为（　　）
A．540B．-540C．20D．-20
7．已知集合A={x||x-1|≥2}，B={x|-2≤x＜2}，则A∩B=（　　）
A．[-2，-1]B．[-1，2）C．[-1，1]D．[1，2）
8．一次考试中，要求考生从试卷上的9个题目中选6个进行答题，则考生不同的选择答题的种数为（　　）
A．6B．84C．504D．69

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网