题目内容
3.已知函数f(x)=$\left\{{\begin{array}{l}{x+2,x>a}\\{{x^2}+5x+2,x≤a}\end{array}}$,若函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是( )| A. | [-1,1) | B. | [-1,2) | C. | [-2,2) | D. | [0,2] |
分析 利用函数的零点,转化为两个函数的图象的交点个数,利用数形结合转化求解即可.
解答  解:函数f(x)=$\left\{{\begin{array}{l}{x+2,x>a}\\{{x^2}+5x+2,x≤a}\end{array}}$,
解:函数f(x)=$\left\{{\begin{array}{l}{x+2,x>a}\\{{x^2}+5x+2,x≤a}\end{array}}$,
x2+5x+2=2x,可得x2+3x+2=0,
解得x=-1,x=-2.y=x+2与y=2x的交点为:
x=2,y=4,
函数y=f(x)与y=2x的图象如图:
函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是:-1≤a<2.
故选:B.
点评 本题考查函数的图象的应用,函数的零点个数的判断,考查数形结合以及计算能力.

练习册系列答案
相关题目
13.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题中假命题的是( )
| A. | 若m⊥α,m⊥β则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m∥α,α∩β=n,则m∥n | D. | 若m⊥α,m?β则 α⊥β |
14.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{3π}{2}$+1+$\frac{\sqrt{3}}{2}$ | B. | 3π+$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | C. | $\frac{3π+1+\sqrt{3}}{2}$ | D. | 3π+1+$\frac{\sqrt{3}}{2}$ |
8.若3a2+3b2-4c2=0,则直线ax+by+c=0被圆x2+y2=1所截得的弦长为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
15.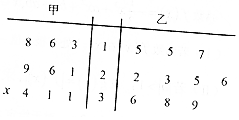 甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示,则“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的( )
甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示,则“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的( )
 甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示,则“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的( )
甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示,则“x=9”是“甲运动员得分平均数大于乙运动员得分平均数”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
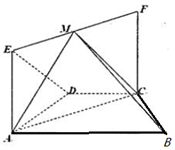 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.