题目内容
18.将5名志愿者分配到3个不同的奥运场馆参加接等工作,每个场馆至少分配一名志愿者的方案种数为( )| A. | 240 | B. | 300 | C. | 150 | D. | 180 |
分析 根据题意,分析有将5个人分成满足题意的3组有1,1,3与2,2,1两种,分别计算可得分成1、1、3与分成2、2、1时的分组情况种数,进而相加可得答案.
解答 解:将5个人分成满足题意的3组有1,1,3与2,2,1两种,
分成1、1、3时,有C53•A33种分法,
分成2、2、1时,有$\frac{{C}_{5}^{2}{C}_{3}^{2}}{{A}_{2}^{2}}$•A33种分法,
所以共有C53•A33+$\frac{{C}_{5}^{2}{C}_{3}^{2}}{{A}_{2}^{2}}$•A33=150种方案,
故选:C.
点评 本题考查组合、排列的综合运用,解题时,注意加法原理与乘法原理的使用.

练习册系列答案
相关题目
9.下列结论正确的是( )
| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}$≥2 | B. | x>0时,6-x-$\frac{4}{x}$的最大值是2 | ||
| C. | $\frac{{x}^{2}+5}{\sqrt{{x}^{2}+4}}$的最小值是2 | D. | 当x∈(0,π)时,sinx+$\frac{4}{sinx}$≥4 |
13.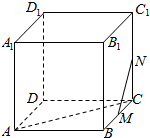 如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )
如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )
 如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )
如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
3.下列不等式一定成立的是( )
| A. | sinx+$\frac{1}{sinx}$≥2 | B. | x2+4≥4|x| | C. | lg(x2+1)>lg(2x) | D. | $\frac{1}{a}$+$\frac{1}{b}$>$\frac{2}{\sqrt{ab}}$ |
10.已知函数f(x)=$\left\{\begin{array}{l}{4x-4(x≤1)}\\{{x}^{2}-4x+3(x>1)}\end{array}\right.$,则f(2)=( )
| A. | 4 | B. | 0 | C. | -1 | D. | 1 |
8.若实数x,y满足不等式组$\left\{\begin{array}{l}{x-2y+4≤0}\\{x+y-11≤0}\\{x≥2}\end{array}\right.$,则$\frac{{y}^{2}}{x}$的最小值为( )
| A. | $\frac{81}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | $\frac{25}{6}$ |