题目内容
 如图,在正方体ABCD-A1B1C1D1中,F为线段BC1的中点,E为线段A1C1上的动点,则下列命题中正确的序号有
如图,在正方体ABCD-A1B1C1D1中,F为线段BC1的中点,E为线段A1C1上的动点,则下列命题中正确的序号有①存在点E使EF∥BD1;
②存在点E使EF⊥平面AB1C1;
③存在点E使EF与AD1所成的角等于90°;
④三棱锥B1-ACE的体积为定值.
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:对于命题①,设存在满足题意的点E,取C1D1的中点G,连结GF,由三角形中位线的性质,推出矛盾,即可作出判断;
对于命题②,在平面AB1C1内找两条相交直线分别垂直于EF即可;
对于命题③,将AD1平移至BC1,只需BC1⊥EF,易知BC1⊥平面A1B1CD,则只需EF?平面A1B1CD,从而可探求点E的存在性;
对于命题④,可考虑三棱锥B1-ACE的底面积与高是否变化,或列出体积的表达式,即可知体积是否为定值.
对于命题②,在平面AB1C1内找两条相交直线分别垂直于EF即可;
对于命题③,将AD1平移至BC1,只需BC1⊥EF,易知BC1⊥平面A1B1CD,则只需EF?平面A1B1CD,从而可探求点E的存在性;
对于命题④,可考虑三棱锥B1-ACE的底面积与高是否变化,或列出体积的表达式,即可知体积是否为定值.
解答:
解:对于命题①,取C1D1的中点G,连结GF,如图1所示.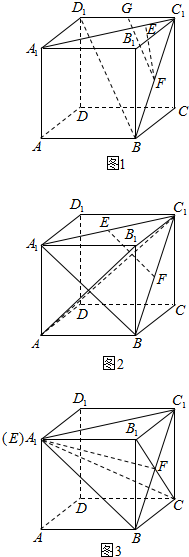
∵F为BC1中点,则FG∥BD1.
设存在点E,使EF∥BD1,于是过点F有两条直线与BD1平行,
∴假设不成立,即不存在点E,使EF∥BD1,故①为假命题.
对于命题②,若E为A1C1的中点,连结A1B,则EF∥A1B.如图2所示.
∵AB1⊥A1B,∴EF⊥AB1,
又∵C1B1⊥平面A1B1BA,AB1?平面A1B1BA,∴C1B1⊥A1B,
∴C1B1⊥EF,又AB1∩C1B1=B1,
∴EF⊥AB1C1,故②为真命题.
对于命题③,当E与A1重合时,连结CE,CB1,A1C,则BC1⊥CB1.如图3所示.
又EB1⊥平面B1C1CB,B1C?平面B1C1CB,∴EB1⊥BC1,
∵EB1∩B1C=B1,∴BC1⊥平面EB1C,
∵EF?平面EB1C,∴BC1⊥EF,
又∵AD1∥BC1,∴AD1⊥EF,
即存在点E,使EF与AD1所成的角等于90°.
对于命题④,设AB=a,则S△ACE=
AC×A1A=
×
a×a=
a2.
∵三棱锥B1-ACE的高即为点B1到平面A1C1CA的距离d,为
a,
∴VB1-ACE=
S△ACE•d=
×
a2×
a=
a3,
即三棱锥B1-ACE的体积为定值,故④为真命题.
综上知,命题中正确的序号有②③④,故答案为②③④.

∵F为BC1中点,则FG∥BD1.
设存在点E,使EF∥BD1,于是过点F有两条直线与BD1平行,
∴假设不成立,即不存在点E,使EF∥BD1,故①为假命题.
对于命题②,若E为A1C1的中点,连结A1B,则EF∥A1B.如图2所示.
∵AB1⊥A1B,∴EF⊥AB1,
又∵C1B1⊥平面A1B1BA,AB1?平面A1B1BA,∴C1B1⊥A1B,
∴C1B1⊥EF,又AB1∩C1B1=B1,
∴EF⊥AB1C1,故②为真命题.
对于命题③,当E与A1重合时,连结CE,CB1,A1C,则BC1⊥CB1.如图3所示.
又EB1⊥平面B1C1CB,B1C?平面B1C1CB,∴EB1⊥BC1,
∵EB1∩B1C=B1,∴BC1⊥平面EB1C,
∵EF?平面EB1C,∴BC1⊥EF,
又∵AD1∥BC1,∴AD1⊥EF,
即存在点E,使EF与AD1所成的角等于90°.
对于命题④,设AB=a,则S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∵三棱锥B1-ACE的高即为点B1到平面A1C1CA的距离d,为
| ||
| 2 |
∴VB1-ACE=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 6 |
即三棱锥B1-ACE的体积为定值,故④为真命题.
综上知,命题中正确的序号有②③④,故答案为②③④.
点评:1.对于点的存在性问题,一般先假设点存在,以此为条件,结合题干,进行推导,若能找到此点,则假设成立,即存在符合题意的点;若得出矛盾,则不存在符合题意的点.
2.对于命题③,也可以由等腰(或等边)三角形A1BC1底边BC1上的中线EF与高线二线合一知,BC1⊥EF,从而AD1⊥EF.
3.处理体积是否为定值问题时,一般思路是:列出体积的表达式,再由表达式探究其是否为定值.
2.对于命题③,也可以由等腰(或等边)三角形A1BC1底边BC1上的中线EF与高线二线合一知,BC1⊥EF,从而AD1⊥EF.
3.处理体积是否为定值问题时,一般思路是:列出体积的表达式,再由表达式探究其是否为定值.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
过点(0,2)且与直线
(t为参数)互相垂直的直线方程为( )
|
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
