题目内容
已知函数f(x)=
,设函数g(x)=f2(x)+f(x)+t,则关于g(x)的零点,下列说法正确的是 .(请填上你认为正确答案的序号)
①t=
时,g(x)有一个零点
②-2<t<
时,g(x)有两个零点
③t=-2时,g(x)有三个零点
④t<-2时,g(x)有四个零点.
|
①t=
| 1 |
| 4 |
②-2<t<
| 1 |
| 4 |
③t=-2时,g(x)有三个零点
④t<-2时,g(x)有四个零点.
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用,不等式的解法及应用
分析:作出函数f(x)的图象,函数的零点个数即为方程解的个数,令g(x)=0,结合条件讨论方程的根的情况,结合图象,即可判断4个选项,可得①②③正确,④错误.
解答:
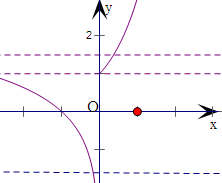 解:作出函数f(x)的图象,如右.
解:作出函数f(x)的图象,如右.
对于①,t=
时,g(x)=f2(x)+f(x)+
,
令g(x)=0,则f(x)=-
,由图象可得y=-
和y=f(x)
只有一个交点,则零点个数为1,故①对;
对于②,-2<t<
时,由f2(x)+f(x)+t=0,
判别式△=1-4t,可得0<
<3,解得f(x)=
,
即有-
<f(x)<1,或-2<f(x)<-
,
由图象可得有两个交点,则有2个零点,故②对;
对于③,t=-2时,g(x)=0,解得f(x)=-2或1,
由图象可得x1=0,x2=-3,x3=-
,则有3个零点,故③对;
对于④,t<-2时,由f2(x)+f(x)+t=0,
判别式△=1-4t,可得
>3,解得f(x)=
,
则有f(x)>1或f(x)<-2,则由图象可得有两个交点,
则有2个零点,故④错.
故答案为:①②③.
 解:作出函数f(x)的图象,如右.
解:作出函数f(x)的图象,如右.对于①,t=
| 1 |
| 4 |
| 1 |
| 4 |
令g(x)=0,则f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
只有一个交点,则零点个数为1,故①对;
对于②,-2<t<
| 1 |
| 4 |
判别式△=1-4t,可得0<
| △ |
-1±
| ||
| 2 |
即有-
| 1 |
| 2 |
| 1 |
| 2 |
由图象可得有两个交点,则有2个零点,故②对;
对于③,t=-2时,g(x)=0,解得f(x)=-2或1,
由图象可得x1=0,x2=-3,x3=-
| 1 |
| 9 |
对于④,t<-2时,由f2(x)+f(x)+t=0,
判别式△=1-4t,可得
| △ |
-1±
| ||
| 2 |
则有f(x)>1或f(x)<-2,则由图象可得有两个交点,
则有2个零点,故④错.
故答案为:①②③.
点评:本题考查分段函数的图象和运用,考查函数的零点的个数,考查数形结合的能力,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
若x、y满足约束条件
,则z=2x+y的最大值为( )
|
| A、12 | ||
| B、4 | ||
C、
| ||
| D、0 |
要得到y=cos2x的图象只需将y=cos(-2x+
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|