题目内容
复平面内,两点M、N所对应的非零复数是α,β(O是原点).
(1)若α2+β2=0,则△OMN是 三角形.
(2)若2α2-2αβ+β2=0,则△OMN是 三角形.
(1)若α2+β2=0,则△OMN是
(2)若2α2-2αβ+β2=0,则△OMN是
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:(1)由α2+β2=0变形得(α+βi)(α-βi)=0,进一步得到α=βi或α=-βi,可得|α|=|±βi|=|β||i|=|β|,得到△OMN是等腰三角形,又设β=x+yi,则α=-y+xi或y-xi,由
•
=0得OM⊥ON.可得△OMN是等腰直角三角形;
(2)根据题意得α2+(α-β)2=0,得[α+(α-β)i][α-(α-β)i]=0,得到|OM|=|MN|,△OMN是等腰三角形,再设α=x+yi,则α-β=±(xi+y),由
•
=0得△OMN是等腰直角三角形.
| OM |
| ON |
(2)根据题意得α2+(α-β)2=0,得[α+(α-β)i][α-(α-β)i]=0,得到|OM|=|MN|,△OMN是等腰三角形,再设α=x+yi,则α-β=±(xi+y),由
| OM |
| ON |
解答:
解:(1)由α2+β2=0,得(α+βi)(α-βi)=0,
∴α=βi或α=-βi,
|α|=|±βi|=|β||i|=|β|,
∴OM=ON,
∴△OMN是等腰三角形,
又设β=x+yi,则α=-y+xi或y-xi,
∴N(x,y),M(-y,x)或(y,-x),
则
•
=-xy+xy=0,∴OM⊥ON.
∴△OMN是直角三角形.
∴△OMN是等腰直角三角形;
(2)根据题意得α2+(α-β)2=0,
∴[α+(α-β)i][α-(α-β)i]=0,
∴|α|=|(α-β)i|
∴|α|=|α-β|,
即|OM|=|MN|.
∴△OMN是等腰三角形,
设α=x+yi,
则α-β=±(xi+y),
∴
•
=0.
∴△OMN是等腰直角三角形.
故答案为:(1)等腰直角三角形;(2)等腰直角三角形.
∴α=βi或α=-βi,
|α|=|±βi|=|β||i|=|β|,
∴OM=ON,
∴△OMN是等腰三角形,
又设β=x+yi,则α=-y+xi或y-xi,
∴N(x,y),M(-y,x)或(y,-x),
则
| OM |
| ON |
∴△OMN是直角三角形.
∴△OMN是等腰直角三角形;
(2)根据题意得α2+(α-β)2=0,
∴[α+(α-β)i][α-(α-β)i]=0,
∴|α|=|(α-β)i|
∴|α|=|α-β|,
即|OM|=|MN|.
∴△OMN是等腰三角形,
设α=x+yi,
则α-β=±(xi+y),
∴
| OM |
| ON |
∴△OMN是等腰直角三角形.
故答案为:(1)等腰直角三角形;(2)等腰直角三角形.
点评:本题考查了复数的代数表示法及其几何意义,考查了平面向量模的求法,是基础的计算题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
若α∈(
,π),则2cos2α=sin(
-α),则sin2α的值为( )
| π |
| 2 |
| π |
| 4 |
A、
| ||
B、-
| ||
| C、1 | ||
D、
|
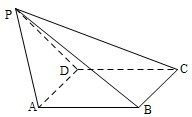 如图,已知四棱锥P-ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
如图,已知四棱锥P-ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.