题目内容
如图(5),已知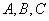 为不在同一直线上的三点,且
为不在同一直线上的三点,且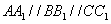 ,
,
 .
.
(1)求证:平面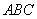 //平面
//平面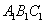 ;
;
(2)若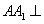 平面
平面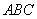 ,且
,且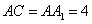 ,
,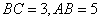 ,
,
求证:A1C丄平面AB1C1
(3)在(2)的条件下,求二面角C1-AB1 -C的余弦值.
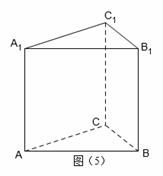
解:(1)证明:∵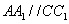 且
且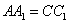
∴四边形 是平行四边形,
是平行四边形,
∴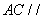
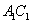 ,∵
,∵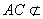 面
面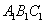 ,
,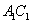
 面
面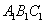
∴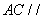 平面
平面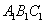 ,
,
同理可得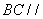 平面
平面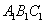 ,又
,又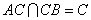 ,
,
∴平面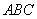 //平面
//平面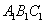
(2)证法1:
∵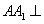 平面
平面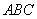 ,
,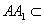 平面
平面 ∴平面
∴平面
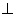 平面
平面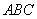 ,
,
平面
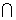 平面
平面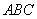 =
=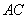 ,
,
∵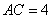 ,
,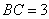 ,
,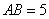 ∴
∴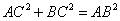 ∴
∴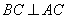
∴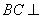 平面
平面
∴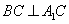 ,∵
,∵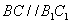 ∴
∴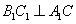
又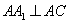 ,
, 得
得 为正方形,∴
为正方形,∴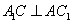
又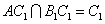 ,
,
∴A1C丄平面AB1C1
【证法2:∵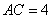 ,
,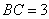 ,
,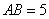 ∴
∴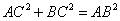 ∴
∴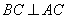 ,
,
 ∵
∵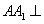 平面
平面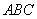 ,
,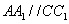 ∴
∴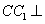 平面
平面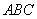
以点C为原点,分别以AC、CB、CC1所在的直线为x、y、z轴建立空间
直角坐标系如图示,由已知可 ,
,
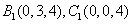 ,
,
则 ,
,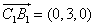
∵ ∴
∴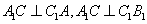
又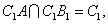 ∴
∴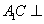 平面
平面 .
.
(3)由(2)得
设平面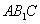 的法向量
的法向量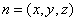 ,则由
,则由 得
得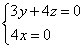 ,
,
令 得
得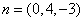
由(2)知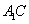 是平面
是平面 的法向量,∴
的法向量,∴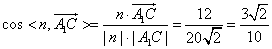 ,
,
即二面角C1-AB1 -C的余弦值为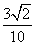 .
.
(其它解法请参照给分)

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
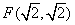 及直线
及直线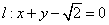 ,曲线
,曲线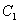 是满足下列两个条件的动点
是满足下列两个条件的动点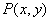 的轨迹:①
的轨迹:① 其中
其中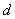 是
是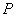 到直线
到直线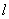 的距离;
的距离;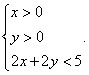
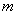 与曲线
与曲线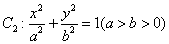 均相切于同一点,求椭圆
均相切于同一点,求椭圆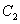 离心率
离心率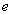 的取值范围.
的取值范围.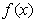 在R上是奇函数,且满足
在R上是奇函数,且满足 ,当
,当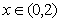 时,
时,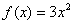 ,则
,则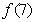 等于 。
等于 。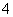 B.
B.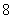 C.
C.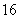 D.
D.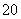

 为方程
为方程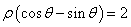 所表示的曲线上一动点,
所表示的曲线上一动点, ,则
,则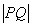 的最小值为 .
的最小值为 . 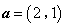 ,
,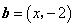 ,若
,若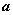 ∥
∥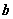 ,
,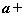
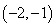
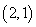
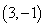
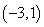
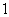 米的正方形,向
米的正方形,向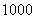 颗黄豆,数得落在正方形区域内
颗黄豆,数得落在正方形区域内
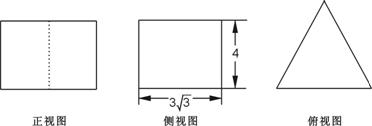
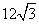 B.
B.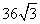 C.
C.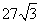 D.6
D.6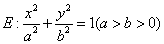 的右焦点为
的右焦点为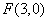 ,过点
,过点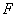 的直线交椭圆于
的直线交椭圆于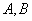 两点.若
两点.若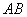 的中点坐标为
的中点坐标为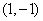 ,则
,则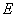 的方程为( )
的方程为( )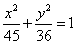 B.
B.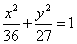 C.
C.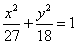 D.
D.