题目内容
在平面直角坐标系中,已知点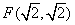 及直线
及直线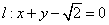 ,曲线
,曲线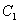 是满足下列两个条件的动点
是满足下列两个条件的动点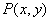 的轨迹:①
的轨迹:① 其中
其中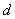 是
是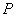 到直线
到直线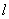 的距离;
的距离;
②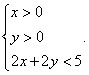
(1) 求曲线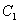 的方程;
的方程;
(2) 若存在直线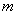 与曲线
与曲线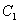 、椭圆
、椭圆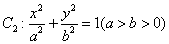 均相切于同一点,求椭圆
均相切于同一点,求椭圆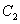 离心率
离心率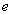 的取值范围.
的取值范围.
解:(1) ,
,
 ,
,
由① 得:
得:
 ,
,
即
将 代入②得:
代入②得: ,
,
解得: 
所以曲线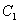 的方程为:
的方程为:

(2)(解法一)由题意,直线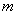 与曲线
与曲线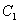 相切,设切点为
相切,设切点为 ,
, 
则直线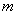 的方程为
的方程为 ,
,
即
将 代入椭圆
代入椭圆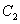 的方程
的方程 ,并整理得:
,并整理得:

由题意,直线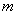 与椭圆
与椭圆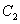 相切于点
相切于点 ,则
,则
 ,
,
即
又 即
即 联解得:
联解得:
由 及
及 得
得
故 ,
,
得 又
又 故
故
所以椭圆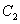 离心率
离心率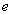 的取值范围是
的取值范围是
(2)(解法二)设直线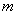 与曲线
与曲线 、椭圆
、椭圆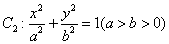 均相切于同一点
均相切于同一点 则
则
由 知
知 ;
;
由 知
知 ,
,
故
联解 ,得
,得
由 及
及 得
得
故 ,
,
得 又
又 故
故
所以椭圆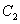 离心率
离心率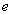 的取值范围是
的取值范围是

练习册系列答案
相关题目
 的离心率为
的离心率为 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线 的焦点重合,过点
的焦点重合,过点 且不垂直于
且不垂直于 轴直线
轴直线 与椭圆
与椭圆 相交于
相交于 、
、 两点.
两点. 的取值范围.
的取值范围. 则
则 ______.
______.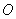 是平面
是平面 内的定点,点
内的定点,点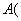 与点
与点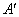 是指:点
是指:点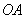 上且
上且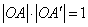 厘米
厘米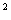 .若平面
.若平面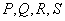 在某不过点
在某不过点 的直线
的直线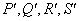 在
在
 中,点
中,点 关于直线
关于直线 的对称点的极坐标为 .
的对称点的极坐标为 . 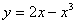 在x=-1处的切线方程为( )
在x=-1处的切线方程为( )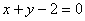 B.
B.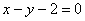 C.
C.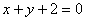 D.
D.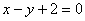
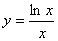 的最大值为( )
的最大值为( )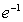 B.
B.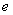 C.
C.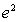 D.
D.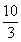
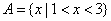 ,
,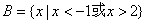 ,则
,则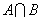 为( )
为( )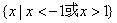 B.
B.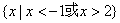 C.
C.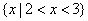 D.R
D.R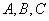 为不在同一直线上的三点,且
为不在同一直线上的三点,且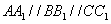 ,
, .
.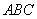 //平面
//平面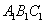 ;
;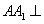 平面
平面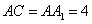 ,
,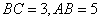 ,
,