题目内容
图(1)中的网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为
A.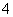 B.
B.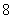 C.
C.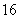 D.
D.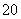

C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
图(1)中的网格纸是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为
A.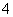 B.
B.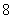 C.
C.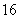 D.
D.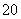

C

 阅读快车系列答案
阅读快车系列答案