题目内容
5.函数f(x)=ax+xlnx在x=1处取得极值.(Ⅰ)求f(x)的单调区间;
(Ⅱ)若y=f(x)-m-1在定义域内有两个不同的零点,求实数m的取值范围.
分析 (Ⅰ)求出函数的导数,计算f′(1),求出a的值,从而求出函数的单调区间即可;
(Ⅱ)问题转化为f(x)=m+1在(0,+∞)内有两个不同的根,结合函数的图象求出m的范围即可.
解答 解:(Ⅰ)f'(x)=a+lnx+1,…(1分)
∵f'(1)=a+1=0,解得a=-1,当a=-1时,f(x)=-x+xlnx,…(2分)
即f'(x)=lnx,令f'(x)>0,解得x>1;…(3分)
令f'(x)<0,解得0<x<1;…(4分)
∴f(x)在x=1处取得极小值,f(x)的增区间为(1,+∞),减区间为(0,1)…(6分)
(Ⅱ)y=f(x)-m-1在(0,+∞)内有两个不同的零点,
可转化为f(x)=m+1在(0,+∞)内有两个不同的根,
也可转化为y=f(x)与y=m+1图象上有两个不同的交点,…(7分)
由(Ⅰ)知,f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
f(x)min=f(1)=-1,…(8分)
由题意得,m+1>-1即m>-2①…(10分)
当0<x<1时,f(x)=x(-1+lnx)<0;
当x>0且x→0时,f(x)→0;
当x→+∞时,显然f(x)→+∞(或者举例:当x=e2,f(e2)=e2>0);
由图象可知,m+1<0,即m<-1②…(11分)
由①②可得-2<m<-1…(12分)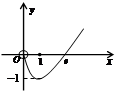
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及数形结合思想、转化思想,是一道中档题.

练习册系列答案
相关题目
15.已知集合P={x|-1≤x≤1},M={a},若P∩M=∅,则a取值范围是( )
| A. | (-∞,-1] | B. | [1,+∞) | C. | [-1,1] | D. | (-∞,-1)∪(1,+∞) |
16.将A,B,C,D这4名同学从左至右随机地排成一排,则“A与B相邻且A与C之间恰好有1名同学”的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
13.已知△ABC中,A=$\frac{π}{6}$,B=$\frac{π}{4}$,a=1,则b等于( )
| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
10.已知数列{an}为等比数列,Sn为其前n项和,且${S_n}=2017×{2016^n}-2018t$,则t=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2019}$ |
1.对于R上可导函数f(x),若满足(x-2)f′(x)>0,则必有( )
| A. | f(1)+f(3)<2f(2) | B. | f(1)+f(3)>2f(2) | C. | f(1)+f(3)>f(0)+f(4) | D. | f(1)+f(0)<f(3)+f(4) |
