题目内容
设无穷等比数列 的公比为q,且
的公比为q,且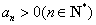 ,
,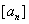 表示不超过实数
表示不超过实数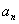 的最大整数(如
的最大整数(如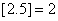 ),记
),记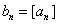 ,数列
,数列 的前
的前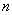 项和为
项和为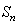 ,数列
,数列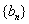 的前
的前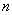 项和为
项和为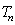 .
.
(Ⅰ)若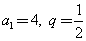 ,求
,求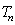 ;
;
(Ⅱ)若对于任意不超过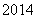 的正整数n,都有
的正整数n,都有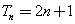 ,证明:
,证明: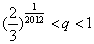 .
.
(Ⅲ)证明: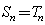 (
(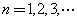 )的充分必要条件为
)的充分必要条件为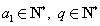 .
.
(Ⅰ) ;(Ⅱ)答案详见解析;(Ⅲ)答案详见解析.
;(Ⅱ)答案详见解析;(Ⅲ)答案详见解析.
【解析】
 即
即 
(Ⅱ)证明:因为  ,所以
,所以  ,
, .
.
因为  ,
,
所以  ,
, .
.

(必要性)因为对于任意的 ,
,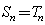 ,
,
当 时,由
时,由 ,得
,得 ;
;
当 时,由
时,由 ,
, ,得
,得 .
.
所以对一切正整数n都有 .
.
由  ,
, ,得对一切正整数n都有
,得对一切正整数n都有 ,
,
所以公比 为正有理数.
为正有理数.
假设  ,令
,令 ,其中
,其中 ,且
,且 与
与 的最大公约数为1.
的最大公约数为1.

因此 ,
, .
.

练习册系列答案
相关题目
 的图象大致是( )
的图象大致是( )
 ,
, ,则
,则 的最小值为 .
的最小值为 .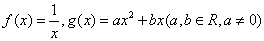 ,若
,若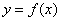 的图象与
的图象与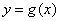 图象有且仅有两个不同的公共点
图象有且仅有两个不同的公共点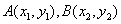 ,则下列判断正确的是
,则下列判断正确的是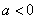 时,
时,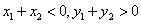 B. 当
B. 当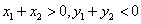
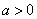 时,
时,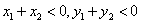 D. 当
D. 当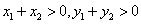
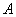 在抛物线
在抛物线 上,且点
上,且点 的距离为
的距离为 ,则点
,则点 B.
B. C.
C. D.
D.
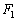 、
、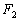 为双曲线
为双曲线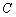 :
: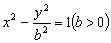 的左、右焦点,过
的左、右焦点,过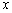 轴的直线,在
轴的直线,在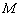 ,且
,且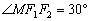 .圆
.圆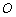 的方程是
的方程是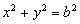 .
.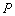 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为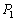 、
、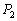 ,求
,求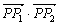 的值;
的值;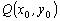 作圆
作圆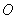 的切线
的切线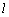 交双曲线
交双曲线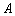 、
、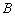 两点,
两点,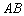 中点为
中点为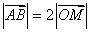 .
.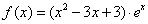 .
.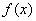 的单调区间;
的单调区间;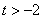 时,判断
时,判断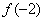 和
和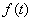 的大小,并说明理由;
的大小,并说明理由;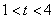 时,关于
时,关于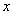 的方程:
的方程: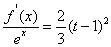 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. 满足
满足 ,则
,则 的值 ( )
的值 ( )
 上是增函数,求实数
上是增函数,求实数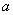 的取值范围.
的取值范围. 的一个极值点,求
的一个极值点,求 上的最大值.
上的最大值.