题目内容
已知函数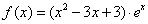 .
.
(1)求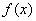 的单调区间;
的单调区间;
(2)当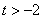 时,判断
时,判断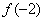 和
和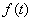 的大小,并说明理由;
的大小,并说明理由;
(3)求证:当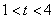 时,关于
时,关于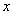 的方程:
的方程: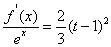 在区间
在区间 上总有两个不同的解.
上总有两个不同的解.
试题分析:(1)
当 时可解得
时可解得 ,或
,或
当 时可解得
时可解得
所以函数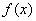 的单调递增区间为
的单调递增区间为 ,
, ,
,
单调递减区间为 3分
3分
(2)当 时,因为
时,因为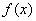 在
在 单调递增,所以
单调递增,所以


所以 在区间
在区间 、
、 分别存在零点,又由二次函数的单调性可知:
分别存在零点,又由二次函数的单调性可知: 最多存在两个零点,所以关于
最多存在两个零点,所以关于 的方程:
的方程: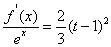 在区间
在区间 上总有两个不同的解………………………….10分
上总有两个不同的解………………………….10分

练习册系列答案
相关题目
 是不等式组
是不等式组 表示的平面区域
表示的平面区域 内的一动点,且不等式
内的一动点,且不等式 总成立,则
总成立,则 的取值范围是_________
的取值范围是_________ _______.
_______.
 的极值
的极值 上恒成立,求
上恒成立,求 的取值范围
的取值范围 ,求证:
,求证:
 的公比为q,且
的公比为q,且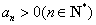 ,
,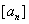 表示不超过实数
表示不超过实数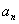 的最大整数(如
的最大整数(如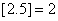 ),记
),记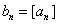 ,数列
,数列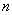 项和为
项和为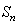 ,数列
,数列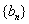 的前
的前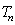 .
.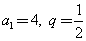 ,求
,求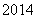 的正整数n,都有
的正整数n,都有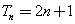 ,证明:
,证明: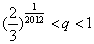 .
.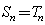 (
(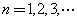 )的充分必要条件为
)的充分必要条件为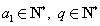 .
.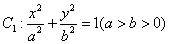 的离心率与双曲线
的离心率与双曲线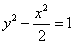 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点为
,右焦点为 ,直线
,直线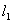 过点
过点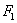 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线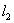 垂直
垂直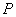 ,线段
,线段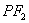 垂直平分线交
垂直平分线交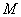 ,求点
,求点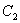 的方程;
的方程;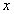 轴交于点
轴交于点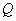 ,不同的两点
,不同的两点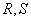 在
在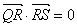 ,求
,求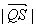 的取值范围.
的取值范围. ,b=log
,b=log ,c=log
,c=log ,则()
,则() 的公差和首项都不等于0,且
的公差和首项都不等于0,且 ,
, ,
, 成等比数列,则
成等比数列,则 ( )
( ) 中,已知
中,已知 ,
, 是
是 上一点,
上一点, ,则
,则
