题目内容
已知sinx+siny=
,求siny-cos2x的最大值.
| 1 |
| 3 |
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:由题意得siny=
-sinx且siny=
-sinx∈[-1,1],得到sinx的取值范围,把所求的式子配方利用二次函数的性质求出其最大值.
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:由已知条件有siny=
-sinx且siny=
-sinx∈[-1,1](结合sinx∈[-1,1])
得-
≤sinx≤1,
而siny-cos2x=
-sinx-cos2x═sin2x-sinx-
令t=sinx(-
≤t≤1),则原式=t2-t-
(-
≤t≤1)
根据二次函数的性质得:当t=-
即sinx=-
时,原式取得最大值
.
| 1 |
| 3 |
| 1 |
| 3 |
得-
| 2 |
| 3 |
而siny-cos2x=
| 1 |
| 3 |
| 2 |
| 3 |
令t=sinx(-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
根据二次函数的性质得:当t=-
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
点评:本题考查同角三角函数的基本关系,正弦函数的有界性,二次函数的性质,求sinx的取值范围是易错点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
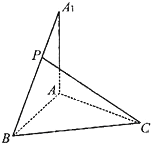 已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.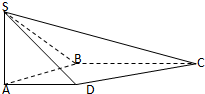 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,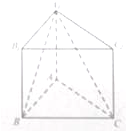 如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=2
如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=2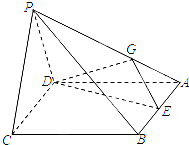 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,平面PCD⊥底面ABCD,E是AB的中点,G为PA上的一点.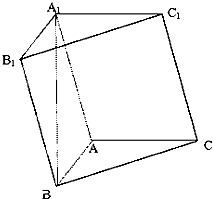 在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.
在三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰好为点B.