题目内容
9.已知函数f(x)=g(x)-(a-1)lnx,g(x)=ax+$\frac{2a-1}{x}$+1-3a+(a-1)lnx.(1)当a=1时,求函数y=f(x)在点(2,f(2))处的切线方程;
(2)若不等式g(x)≥0在x∈[1,+∞)时恒成立,求正实数a的取值范围.
分析 (1)当a=1时,求导数,确定切线的斜率,即可求出切线方程;
(2)求出函数的导数,分类讨论,利用g′(x)≥0在x∈[1,+∞)时恒成立,即可得出结论.
解答 解:(1)当a=1时,f(x)=x+$\frac{1}{x}$-2,f′(x)=1-$\frac{1}{{x}^{2}}$,
∴f′(2)=$\frac{3}{4}$,f(2)=$\frac{1}{2}$,
∴函数y=f(x)在点(2,f(2))处的切线方程为y-$\frac{1}{2}$=$\frac{3}{4}$(x-2),
即3x-4y-4=0;
(2)g′(x)=$\frac{a(x-1)[x-(\frac{1}{a}-2)]}{{x}^{2}}$,
0<a<$\frac{1}{3}$时,g′(x)>0,得x>$\frac{1}{a}$-2,
令g′(x)<0,得1<x<$\frac{1}{a}$-2,
∴g(x)在(1,$\frac{1}{a}$-2)上是减函数,
∴x∈(1,$\frac{1}{a}$-2),g(x)<g(1)=0,
与g(x)≥0在x∈[1,+∞)时恒成立矛盾,
a≥$\frac{1}{3}$,g′(x)≥0在x∈[1,+∞)时恒成立,
g(x)在[1,+∞)为增函数,
∴g(x)≥g(1)=0,符合题意,
综上所述,a≥$\frac{1}{3}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.圆C1:x2+y2-4x-2y+1=0与圆C2:x2+y2+4x-8y+11=0的位置关系为( )
| A. | 相交 | B. | 相离 | C. | 外切 | D. | 内切 |
2.如图,已知$\overrightarrow{AB}$=a,$\overrightarrow{AC}$=b,$\overrightarrow{BD}$=3 $\overrightarrow{DC}$,用$\vec a$,$\vec b$表示$\overrightarrow{AD}$,则$\overrightarrow{AD}$=( )


| A. | $\vec a$+$\frac{3}{4}$$\vec b$ | B. | $\frac{1}{4}$ $\vec a$+$\frac{3}{4}$$\vec b$ | C. | $\frac{1}{4}$ $\vec a$+$\frac{1}{4}$$\vec b$ | D. | $\frac{3}{4}$ $\vec a$+$\frac{1}{4}$$\vec b$ |
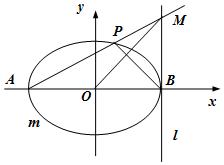 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.