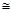题目内容
在如图所示的几何体中,四边形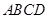 是等腰梯形,
是等腰梯形,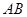 ∥
∥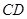 ,
,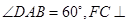 平面
平面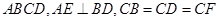 .
.
(Ⅰ)求证: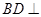 平面
平面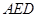 ;
;
(Ⅱ)求二面角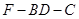 的余弦值.
的余弦值.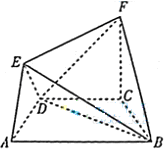
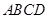 是等腰梯形,
是等腰梯形,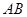 ∥
∥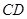 ,
,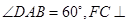 平面
平面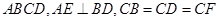 .
.(Ⅰ)求证:
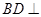 平面
平面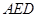 ;
;(Ⅱ)求二面角
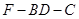 的余弦值.
的余弦值.
:(Ⅰ)见解析;(Ⅱ)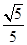
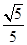
:(Ⅰ)如图,因为 是等腰三角形,且
是等腰三角形,且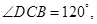 所以
所以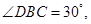
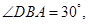
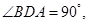 即
即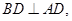 又
又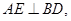 所以
所以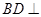 平面
平面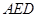 .
.
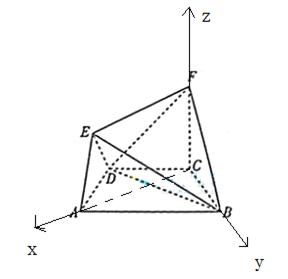
(Ⅱ)如图,连结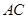 ,则
,则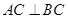 ,建立空间直角坐标系,设
,建立空间直角坐标系,设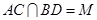 ,
,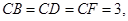 则
则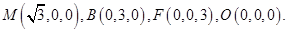
设平面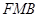 的法向量为
的法向量为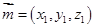 ,则
,则
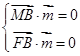 ,所以
,所以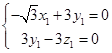 ,令
,令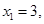 得
得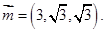
而平面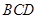 的一个法向量为
的一个法向量为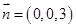
由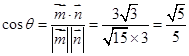 可得
可得
二面角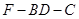 的余弦值为
的余弦值为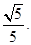
【考点定位】本题结合熟知的等腰梯形这一底面考查了空间线面垂直的判定方法,通过建立空间直角坐标系考查了向量法求二面角的方法,等腰梯形这一底面是建立空间坐标系的基础,解题时要善于发现垂直关系
 是等腰三角形,且
是等腰三角形,且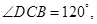 所以
所以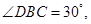
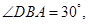
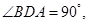 即
即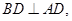 又
又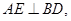 所以
所以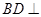 平面
平面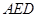 .
.(Ⅱ)如图,连结
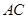 ,则
,则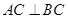 ,建立空间直角坐标系,设
,建立空间直角坐标系,设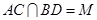 ,
,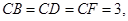 则
则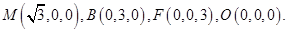

设平面
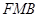 的法向量为
的法向量为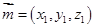 ,则
,则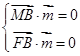 ,所以
,所以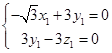 ,令
,令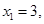 得
得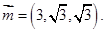
而平面
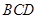 的一个法向量为
的一个法向量为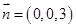
由
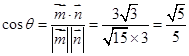 可得
可得二面角
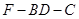 的余弦值为
的余弦值为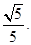
【考点定位】本题结合熟知的等腰梯形这一底面考查了空间线面垂直的判定方法,通过建立空间直角坐标系考查了向量法求二面角的方法,等腰梯形这一底面是建立空间坐标系的基础,解题时要善于发现垂直关系

练习册系列答案
相关题目
 面ABC,BC
面ABC,BC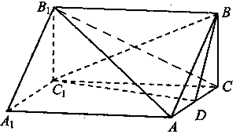
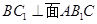 ;
;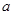 、
、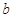 、
、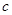 表示三条不同的直线,
表示三条不同的直线,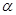 表示平面,给出下列命题:
表示平面,给出下列命题: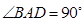 ,AD∥BC, AB="BC=2," AD="4,"
,AD∥BC, AB="BC=2," AD="4," 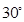 角,E是PD的中点.
角,E是PD的中点. 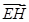 的坐标;
的坐标;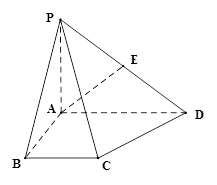
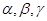 ,直线
,直线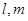 满足:
满足: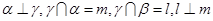 ,那么
,那么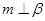 ; ②
; ②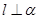 ; ③
; ③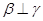 ; ④
; ④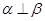 。
。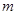 ,
,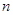 为两条不同的直线,
为两条不同的直线,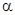 ,
,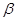 为两个不同的平面,则下列命题是真命题的是( )
为两个不同的平面,则下列命题是真命题的是( )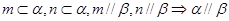
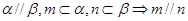
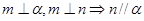
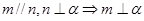
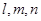 是三条不同的直线,
是三条不同的直线,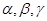 是三个不同的平面,现给出四个命题:
是三个不同的平面,现给出四个命题: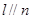 且
且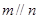 ,则
,则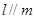 ; ②若
; ②若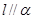 且
且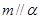 ,则
,则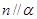 且
且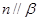 ,则
,则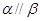 ; ④若
; ④若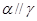 且
且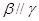 ,则
,则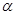 、
、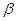 是两个不同的平面,则下列说法正确的是
是两个不同的平面,则下列说法正确的是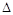 ABC
ABC