题目内容
【题目】给出集合![]() .
.
(1)若![]() ,求证:函数
,求证:函数![]() ;
;
(2)由(1)分析可知, ![]() 是周期函数且是奇函数,于是张三同学得出两个命
是周期函数且是奇函数,于是张三同学得出两个命
题:命题甲:集合![]() 中的元素都是周期函数.命题乙:集合
中的元素都是周期函数.命题乙:集合![]() 中的元素都是奇函数. 请对此
中的元素都是奇函数. 请对此
给出判断,如果正确,请证明;如果不正确,请举反例;
(3)若![]() ,数列
,数列![]() 满足:
满足: ![]() ,且
,且![]()
![]() ,数列
,数列![]() 的前
的前![]() 项
项
和为![]() ,试问是否存在实数
,试问是否存在实数![]() 、
、![]() ,使得任意的
,使得任意的![]() ,都有
,都有![]() 成立,若
成立,若
存在,求出![]() 、
、![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
【答案】(1)见解析(2)命题甲正确(3)![]()
【解析】试题分析:
(1)原问题即![]() ,结合两角和差正余弦公式整理变形即可证得题中的结论;
,结合两角和差正余弦公式整理变形即可证得题中的结论;
(2)由题意可得:命题甲正确. 集合![]() 中的元素都是周期为6的周期函数.命题乙不正确.如
中的元素都是周期为6的周期函数.命题乙不正确.如![]() 是奇函数;
是奇函数; ![]() 不是奇函数.
不是奇函数.
(3)由题意可得![]() ,假设存在实数
,假设存在实数![]() 满足题设,据此计算可得
满足题设,据此计算可得![]() ,即数列
,即数列![]() 是周期为
是周期为![]() 的周期数列,且前6项依次为
的周期数列,且前6项依次为![]() ,据此可知
,据此可知![]() ,则满足题意时只需
,则满足题意时只需![]() 即可.
即可.
试题解析:
(1)![]() 转化证明
转化证明
![]()
![]()
左边![]()
![]()
![]() 右边
右边
(2)命题甲正确. 集合![]() 中的元素都是周期为6的周期函数.
中的元素都是周期为6的周期函数.
验证![]() 即可
即可
命题乙不正确.集合![]() 中的元素不都是奇函数.
中的元素不都是奇函数.
如![]() 是奇函数;
是奇函数; ![]() 不是奇函数.
不是奇函数.
(3)![]()
![]() ,则
,则![]()
![]()
假设存在实数![]() 满足题设,则
满足题设,则
![]()
![]()
![]()
所以数列![]() 是周期为
是周期为![]() 的周期数列,且前6项依次为
的周期数列,且前6项依次为![]()
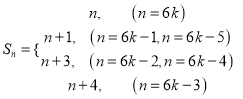
![]()
当![]() ,
, ![]() 时,
时, ![]()
当![]()
![]() 时,
时, ![]()
![]()
当![]()
![]() 时,
时, ![]()
![]()
当![]()
![]() 时,
时, ![]()
![]()
综上![]()
要使对任意的![]() ,都有
,都有![]() 恒成立,
恒成立,
只要![]() 即可.
即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


