题目内容
【题目】(本题![]() 分)
分)
已知函数![]() ,若存在
,若存在![]() ,使得
,使得![]() ,则称
,则称![]() 是函数
是函数![]() 的一个不动点,设二次函数
的一个不动点,设二次函数![]() .
.
(Ⅰ)当![]() ,
, ![]() 时,求函数
时,求函数![]() 的不动点.
的不动点.
(Ⅱ)若对于任意实数![]() ,函数
,函数![]() 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)在(![]() )的条件下,若函数
)的条件下,若函数![]() 的图象上
的图象上![]() ,
, ![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且直线
的不动点,且直线![]() 是线段
是线段![]() 的垂直平分线,求实数
的垂直平分线,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)实数
(3)实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:Ⅰ)把![]() ,
, ![]() 代入方程f(x)=x,解出x即可;
代入方程f(x)=x,解出x即可;
(Ⅱ)方程f(x)=x恒有两个不相等的实数根,即方程ax2+(b+1)x+b﹣2=x恒有两个不相等的实数根,则 ![]() 对任意b恒成立,根据二次函数的性质可得a的不等式;
对任意b恒成立,根据二次函数的性质可得a的不等式;
(Ⅲ)设函数f(x)的两个不同的不动点为x1,x2,则A(x1,x1),B(x2,x2),且x1,x2是ax2+bx+b﹣2=0的两个不等实根,则![]() ,由题意可得k=﹣1,且AB中点
,由题意可得k=﹣1,且AB中点![]() 在直线
在直线![]() 上,代入可得a,b的关系式,分离出b后根据a的范围可得b的范围;
上,代入可得a,b的关系式,分离出b后根据a的范围可得b的范围;
试题解析:
(Ⅰ)当![]() ,
, ![]() 时,
时, ![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() 或
或![]() .
.
∴函数![]() 的不动点为
的不动点为![]() ,
, ![]() .
.
(Ⅱ)∵对于任意实数![]() ,函数
,函数![]() 恒有两个不同的不动点,
恒有两个不同的不动点,
∴对于任意实数![]() ,方程
,方程![]() 恒有两个不相等的实数根,
恒有两个不相等的实数根,
即方程![]() 恒有两个不相等的实数根,
恒有两个不相等的实数根,
∴![]() ,即对任意实数
,即对任意实数![]() ,
, ![]() 恒成立,
恒成立,
∴![]() ,
,
解得![]() .
.
(Ⅲ)设函数![]() 的两个不同的不动点为
的两个不同的不动点为![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的两个不等实根,
的两个不等实根,
所以![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,线段
,线段![]() 中点坐标为
中点坐标为![]() ,
,
∵直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ,且
,且![]() 在直线
在直线![]() 上,
上,
即![]() ,
, ![]() ,
,
∴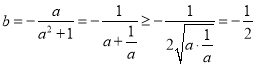 ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
又∵![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目