题目内容
在Rt△ABC中,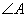 为直角,已知BC=a,若长为2a的线段PQ以点A为中点,问
为直角,已知BC=a,若长为2a的线段PQ以点A为中点,问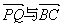 的夹角
的夹角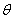 取何值时
取何值时 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
解:(1)由 得
得 ,
, ,
,
(2)证明:由(1)得 ,
,
任取 ,且
,且 (1分)
(1分)
则 =
=
所以 在
在 上是单调递增函数
上是单调递增函数
(3)因为偶函数 在
在 上是单调递增函数,又
上是单调递增函数,又 ,
,
①当 时,得
时,得 在
在 上有且只有一个实根,所以函数
上有且只有一个实根,所以函数 的图象有且只有一个交点,由图象得
的图象有且只有一个交点,由图象得 ;
;
②当 时,得
时,得 在
在 上有且只有一个实根,所以函数
上有且只有一个实根,所以函数 的图象有且只有一个交点,由图象得
的图象有且只有一个交点,由图象得 。
。
综上所述:
 22.
22.


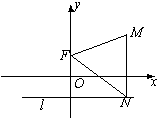
解法二:以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.




练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
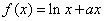 存在与直线
存在与直线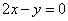 平行的切线,则实数
平行的切线,则实数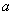 的取值范围
的取值范围 的方程
的方程 恒有实数解,则实数
恒有实数解,则实数 的取值范围是( )
的取值范围是( ) B.
B.  C.
C.  D.
D. 
 ,且
,且 在区间
在区间 有最小
有最小 值为( )
值为( ) B.
B.  C.
C.  D.
D. 
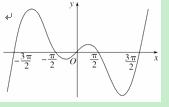
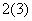 =-f(x),且函数y=f
=-f(x),且函数y=f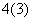 为奇函数,给出以下四个命题:
为奇函数,给出以下四个命题: 对称;
对称; f(x)为R上的偶函数;
f(x)为R上的偶函数;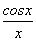
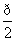 )(x-
)(x-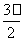 )
) 是定义域为
是定义域为 的偶函数. 当
的偶函数. 当 时,
时, ,
,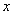 的方程
的方程 (
( ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
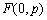 ,直线
,直线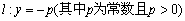 ,
,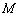 为平面内的动点,过
为平面内的动点,过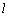 的垂线,垂足为
的垂线,垂足为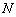 ,且
,且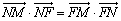 .
. 的方程;
的方程;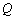 是
是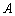 、
、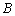 .
.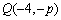 ,
,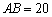 ,求
,求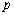 的值.
的值.