题目内容
已知抛物线y2=4x,直线l:y=-
x+b与抛物线交于A,B两点.
(Ⅰ)若x轴与以AB为直径的圆相切,求该圆的方程;
(Ⅱ)若直线l与y轴负半轴相交,求△AOB面积的最大值.
| 1 |
| 2 |
(Ⅰ)若x轴与以AB为直径的圆相切,求该圆的方程;
(Ⅱ)若直线l与y轴负半轴相交,求△AOB面积的最大值.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)联立
得y2+8y-8b=0.由此利用根的判别式、弦长公式,结合已知条件能求出圆的方程.
(Ⅱ)由直线l与y轴负半轴相交,得-1<b<0,由点O到直线l的距离d=
,得S△AOB=
|AB|d=4
.由此利用导数性质能求出△AOB的面积的最大值.
|
(Ⅱ)由直线l与y轴负半轴相交,得-1<b<0,由点O到直线l的距离d=
| -2b | ||
|
| 1 |
| 2 |
| 2 |
| b3+2b2 |
解答:
解:(Ⅰ)联立
得:y2+8y-8b=0.
依题意应有△=64+32b>0,解得b>-2.
设A(x1,y1),B(x2,y2),
设圆心Q(x0,y0),则应有x0=
,y0=
=-4.
因为以AB为直径的圆与x轴相切,得到圆半径为r=|y0|=4,
又|AB|=
=
.
所以|AB|=2r,
即
=8,
解得b=-
.
所以x0=
=2b+8=
,
所以圆心为(
,-4).
故所求圆的方程为(x-
)2+(y+4)2=16..
(Ⅱ)因为直线l与y轴负半轴相交,
∴b<0,
又l与抛物线交于两点,由(Ⅰ)知b>-2,
∴-2<b<0,
直线l:y=-
x+b整理得x+2y-2b=0,点O到直线l的距离d=
=
,
所以∴S△AOB=
|AB|d=-4b
=4
.
令g(b)=b3+2b2,-2<b<0,
g′(b)=3b2+4b=3b(b+
),
∴g(b)在(-2,-
)增函数,在(-
,0)是减函数,
∴g(b)的最大值为g(-
)=
.
∴当b=-
时,△AOB的面积取得最大值
.
|
依题意应有△=64+32b>0,解得b>-2.
设A(x1,y1),B(x2,y2),
设圆心Q(x0,y0),则应有x0=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
因为以AB为直径的圆与x轴相切,得到圆半径为r=|y0|=4,
又|AB|=
| (1+4)[(y1+y2)2-4y1•y2] |
| 5(64+32b) |
所以|AB|=2r,
即
| 5(64+32b) |
解得b=-
| 8 |
| 5 |
所以x0=
| x1+x2 |
| 2 |
| 24 |
| 5 |
所以圆心为(
| 24 |
| 5 |
故所求圆的方程为(x-
| 24 |
| 5 |
(Ⅱ)因为直线l与y轴负半轴相交,
∴b<0,
又l与抛物线交于两点,由(Ⅰ)知b>-2,
∴-2<b<0,
直线l:y=-
| 1 |
| 2 |
| |-2b| | ||
|
| -2b | ||
|
所以∴S△AOB=
| 1 |
| 2 |
| 2 |
| 2+b |
| 2 |
| b3+2b2 |
令g(b)=b3+2b2,-2<b<0,
g′(b)=3b2+4b=3b(b+
| 4 |
| 3 |
∴g(b)在(-2,-
| 4 |
| 3 |
| 4 |
| 3 |
∴g(b)的最大值为g(-
| 4 |
| 3 |
| 32 |
| 27 |
∴当b=-
| 4 |
| 3 |
32
| ||
| 9 |
点评:本题主要考查圆的方程的求法,考查三角形面积的最大值的求法,考查直线与抛物线、圆等知识,同时考查解析几何的基本思想方法和运算求解能力.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知两个不同的平面和两条不重合的直线,有下列四个命题
①若m∥n,n?α,则m∥α
②若a⊥β,α⊥β,则a∥α
③若a⊥b,a⊥α,b⊥β,则α⊥β
④若m⊥n,α∥β,m⊥α,则n∥β
则以上命题错误的个数为( )
①若m∥n,n?α,则m∥α
②若a⊥β,α⊥β,则a∥α
③若a⊥b,a⊥α,b⊥β,则α⊥β
④若m⊥n,α∥β,m⊥α,则n∥β
则以上命题错误的个数为( )
| A、1个 | B、2个 | C、2个 | D、4个 |
若3sinα+cosα=0,则
的值为( )
| 1 |
| cos2α+sin2α |
A、
| ||
B、
| ||
C、
| ||
| D、-2 |
已知
=(λ,2),
=(-3,5),且
与
的夹角为锐角,则λ的取值范围( )
| a |
| b |
| a |
| b |
A、λ<
| ||||
B、λ≥
| ||||
C、λ<
| ||||
D、λ≤
|
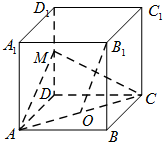 在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.
在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.