题目内容
设命题p:函数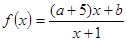 在(0,+
在(0,+ )上是增函数;命题q:方程
)上是增函数;命题q:方程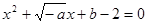 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。
(1)求点P(a,b)的轨迹图形的面积;
(2)求a+5b的取值范围。
(1) (2) (7,
(2) (7,  )
)
解析试题分析:解:(1)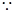 f(x) =
f(x) = ,f ′(x)=
,f ′(x)=  ,
, p真
p真 x
x (0,+
(0,+ )时,
)时, >0
>0 a-b+5>0,(2′)
a-b+5>0,(2′) 方程x2+
方程x2+ x+b-2=0有两个不相等的负实数根
x+b-2=0有两个不相等的负实数根



 ,
,
即q真
 ; 5分
; 5分
若p q是真命题。则p真q真,
q是真命题。则p真q真,
 点P(a,b)的轨迹图形如图,
点P(a,b)的轨迹图形如图, ABC
ABC
的内部;(8′) 由边界可得A(0,2),B(-3,2),C(- ,
, )
)
 ABC的面积S=
ABC的面积S=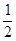
 3
3 (
( -2)=
-2)= ,
,
即点P(a,b)的轨迹图形的面积为 ; 10分
; 10分
(2)设a+5b="z," 直线a+5b=z过B点时,z=-3+5 2=7,直线a+5b=z过C点时,
2=7,直线a+5b=z过C点时,
z=- +5
+5
 =
= ,
, a+5b的取值范围是(7,
a+5b的取值范围是(7,  ) 13分
) 13分
考点:线性规划的运用
点评:解决的关键是能得到关于a,b的不等式组,然后作出可行域,结合图像来求解面积和最值,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :方程
:方程 有两个不等的负根,
有两个不等的负根, :方程
:方程 无实根,若p或q为真,p且q为假,求
无实根,若p或q为真,p且q为假,求 的取值范围.
的取值范围. ,设命题
,设命题 :函数
:函数 在区间
在区间 上与
上与 轴有两个不同的交点;命题
轴有两个不同的交点;命题 :
: 在区间
在区间 上有最小值.若
上有最小值.若 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围. :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 有实数根;如果“
有实数根;如果“ ”为假,且“
”为假,且“ ”为真,求实数
”为真,求实数 的取值范围。
的取值范围。 ;
; 若
若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围。
的取值范围。 交椭圆
交椭圆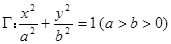 于
于 两点,交直线
两点,交直线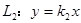 于点
于点 .
. 的中点,求证:
的中点,求证: ;
; :
: 和条件
和条件 :
: ,请选取适当的实数
,请选取适当的实数 的值,分别利用所给的两个条件作为
的值,分别利用所给的两个条件作为 、
、 构造命题“若
构造命题“若 ;命题
;命题 ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。