题目内容
已知 ,设命题
,设命题 :函数
:函数 在区间
在区间 上与
上与 轴有两个不同的交点;命题
轴有两个不同的交点;命题 :
: 在区间
在区间 上有最小值.若
上有最小值.若 是真命题,求实数
是真命题,求实数 的取值范围.
的取值范围.
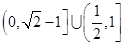
解析试题分析:先由 的真假性确定命题
的真假性确定命题 为假命题,
为假命题, 为真命题,然后就命题
为真命题,然后就命题 为真命题进行求解,结合二次函数的零点分布来讨论,最后在取答案时取参数范围的在
为真命题进行求解,结合二次函数的零点分布来讨论,最后在取答案时取参数范围的在 上的补集;对命题
上的补集;对命题 为真命题对
为真命题对 的范围进行求解,对于函数
的范围进行求解,对于函数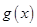 解析式化为分段函数,利用分段函数的单调性来考查.
解析式化为分段函数,利用分段函数的单调性来考查.
试题解析:要使函数 在
在 上与
上与 轴有两个不同的交点,
轴有两个不同的交点,
必须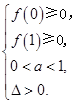 2分
2分
即 4分
4分
解得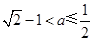 .
.
所以当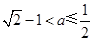 时,函数
时,函数 在
在 上与
上与 轴有两个不同的交点. 5分
轴有两个不同的交点. 5分
下面求 在
在 上有最小值时
上有最小值时 的取值范围:
的取值范围:
方法1:因为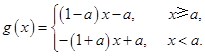 6分
6分
①当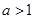 时,
时,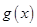 在
在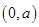 和
和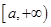 上单调递减,
上单调递减,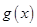 在
在 上无最小值; 7分
上无最小值; 7分
②当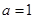 时,
时,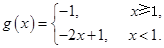
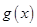 在
在 上有最小值
上有最小值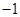 ; 8分
; 8分
③当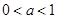 时,
时,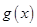 在
在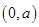 上单调递减,在
上单调递减,在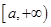 上单调递增,
上单调递增,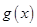 在
在 上有最小值
上有最小值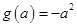 . 9分
. 9分
所以当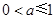 时,函数
时,函数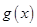 在
在 上有最小值. 10分
上有最小值. 10分
方法2:因为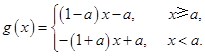 6分
6分
因为 ,所以
,所以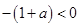 .
.
所以函数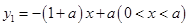 是单调递减的. 7分
是单调递减的. 7分
要使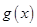 在
在 上有最小值,必须使
上有最小值,必须使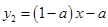 在
在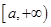 上单调递增或为常数. 8分
上单调递增或为常数. 8分
即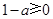 ,即
,即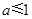 . 9分
. 9分
所以当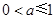 时,函数
时,函数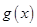 在
在 上有最小值. 10分
上有最小值. 10分
若 是真命题,则
是真命题,则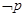 是真命题且
是真命题且
练习册系列答案
相关题目
 x∈[1,2],x2-a≥0;命题q:
x∈[1,2],x2-a≥0;命题q: x0∈R,使得x+(a-1)x0+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围。
x0∈R,使得x+(a-1)x0+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围。 ,且
,且 ,命题
,命题 ,且
,且 .
. ,求实数
,求实数 的值;
的值; 是
是 的充分条件,求实数
的充分条件,求实数 ,
, ,命题
,命题 ,使得
,使得 .若“
.若“ 或
或 为真”,“
为真”,“ 的取值范围.
的取值范围.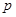 :实数
:实数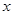 满足
满足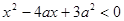 ,其中
,其中 ;命题
;命题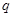 :实数
:实数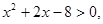 且
且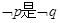 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围. 且
且 ,则
,则 ”是真命题还是假命题,并证明你的结论.
”是真命题还是假命题,并证明你的结论.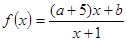 在(0,+
在(0,+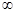 )上是增函数;命题q:方程
)上是增函数;命题q:方程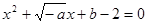 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。 :实数
:实数 满足
满足 , 命题
, 命题 :实数
:实数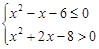 .
. 为真,求实数
为真,求实数