题目内容
(本题满分16分) 本题共有3个小题,第1小题满分7分,第2小题满分7分,第3小题满分2分.
设直线 交椭圆
交椭圆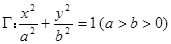 于
于 两点,交直线
两点,交直线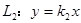 于点
于点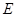 .
.
(1)若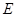 为
为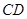 的中点,求证:
的中点,求证: ;
;
(2)写出上述命题的逆命题并证明此逆命题为真;
(3)请你类比椭圆中(1)、(2)的结论,写出双曲线中类似性质的结论(不必证明).
(1)设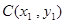
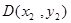
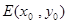 ,
,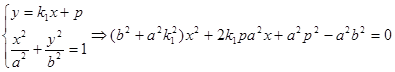
 ,
,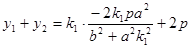
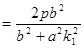
又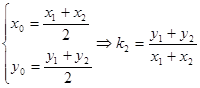
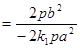

(2)逆命题:设直线 交椭圆
交椭圆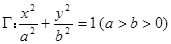 于
于 两点,交直线
两点,交直线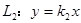 于点
于点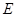 .若
.若 ,则
,则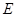 为
为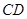 的中点.
的中点.
证明:由方程组
因为直线 交椭圆
交椭圆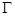 于
于 两点,
两点,
所以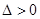 ,即
,即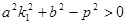 ,设
,设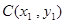 、
、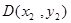 、
、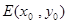
则 ,
,
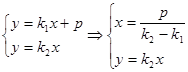 又因为
又因为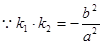 ,所以
,所以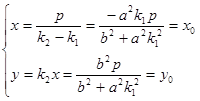 ,故E为CD的中点.
,故E为CD的中点.
(3)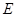 为
为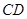 中点的充要条件是
中点的充要条件是 .
.
解析试题分析:(1)解法一:设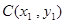
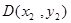
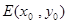

 ,
,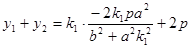
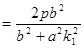
又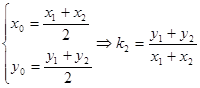
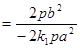

解法二(点差法):设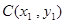
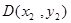
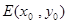
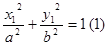 ,
,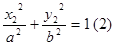
两式相减得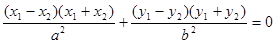
即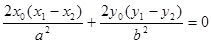
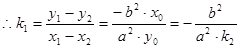

(2)逆命题:设直线 交椭圆
交椭圆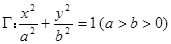 于
于 两点,交直线
两点,交直线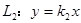 于点
于点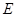 .若
.若 ,则
,则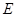 为
为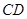 的中点.
的中点.
证法一:由方程组
因为直线 交椭圆
交椭圆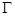 于
于 两点,
两点,
所以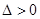 ,即
,即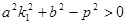 ,设
,设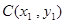 、
、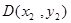 、
、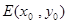
则 ,
,
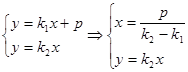 又因为
又因为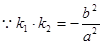 ,所以
,所以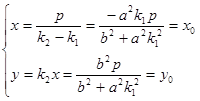 ,故E为CD的中点.
,故E为CD的中点.
证法二:设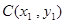
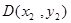
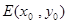
则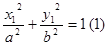 ,
,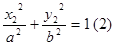
两式相减得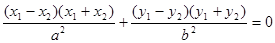
即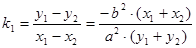
又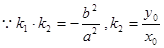 ,
,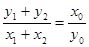 即
即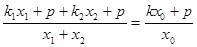
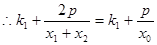
得
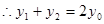 ,即
,即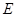 为
为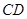 的中点.
的中点.
(3)设直线 交双曲线
交双曲线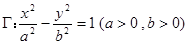 于
于 两点,交直线
两点,交直线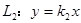 于点
于点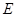 .则
.则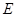 为
为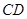 中点的充要条件是
中点的充要条件是 .
.
考点:本题考查了直线与圆锥曲线的位置关系
点评:求过定点的圆锥曲线的中点弦问题,通常有下面两种方法:(1)点差法,即设出弦的两端点的坐标代入圆锥曲线方程后相减,得到弦中点坐标与弦所在直线斜率的关系,从而求出直线方程.(2)联立法,即将直线方程与双曲线方程联立,利用韦达定理与判别式求解.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 :方程
:方程 无实根,命题
无实根,命题 :方程
:方程 是焦点在
是焦点在 轴上的椭圆.若
轴上的椭圆.若 与
与 同时为假命题,求
同时为假命题,求 的取值范围.
的取值范围.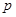 :实数
:实数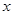 满足
满足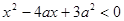 ,其中
,其中 ;命题
;命题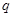 :实数
:实数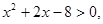 且
且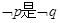 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围. ,q:
,q: ,若
,若 是
是 的充分而不必要条件,求实数
的充分而不必要条件,求实数 的取值范围.
的取值范围.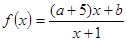 在(0,+
在(0,+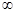 )上是增函数;命题q:方程
)上是增函数;命题q:方程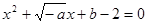 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。 :实数
:实数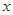 满足
满足 ,其中
,其中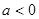 ;命题
;命题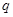 :实数
:实数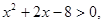 且
且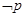 是
是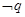 的必要不充分条件,求实数
的必要不充分条件,求实数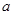 的取值范围.
的取值范围.  则
则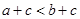 ”. ( 其中
”. ( 其中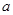 、
、 、
、 )
) 在(-1, +
在(-1, +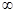 )上单调递增, 命题
)上单调递增, 命题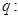 函数y=lg[
函数y=lg[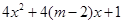 ]的定义域为R
]的定义域为R 或
或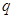 ”为真命题,求
”为真命题,求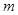 的取值范围;
的取值范围;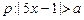 ,(
,(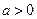 )和条件
)和条件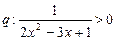 ,
,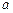 的取值范围,使命题:“
的取值范围,使命题:“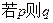 ”为真命题,它的逆命题为假命题。
”为真命题,它的逆命题为假命题。