Question

【题目】已知函数（）

（1）若为的极大值点，求的取值范围；.

（2）当时，判断与轴交点个数，并给出证明.

Answer 1

【答案】（1）（2）有唯一零点；证明见解析；

【解析】

（1）求出,对与的大小关系进行讨论，得出函数的单调性，分析其函数的极值，得出答案.

（2）讨论与轴交点个数,由即讨论的实数根的个数，设，分析出函数的单调性，分析出函数值的情况，得出答案.

（1）

设，，所以在上单调递增.

当时，，当时，，当时，，

所以当时，，单调递增，当时，，单调递增,所以此时无极值.

当时，，

则一定存在，使得

所以当时，，从而，单调递减.

当时，，从而单调递增.

所以此时满足为的极大值点

当时，，

所以当时，，从而，所以在单调递增

此时不可能为的极大值点.

综上所述：当为的极大值点时，的取值范围是.

（2）讨论与轴交点个数,即讨论方程的根的个数.

设，则

令，得，令，得

所以在上单调递减，在上单调递增,所以

所以讨论方程的根的个数，即探讨的实数根的个数.

设，

则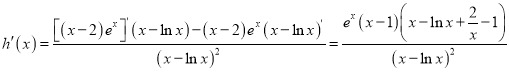

设，则

令，得，令，得

所以在上单调递减，在上单调递增.所以

所以当时，，当时，

所以在上单调递减，在上单调递增

又当时，，且，

当时，且时，

所以当时，方程有唯一实数根.

综上：，与轴有唯一交点