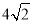题目内容
10.若在区间[-3,2]内随机取一个整数m,在区间[-2,3]内随机取一个整数n,则使得方程x2+mx-$\frac{1}{4}$n2+$\frac{3}{4}$=0有两个不同的实数根的概率1-$\frac{3π}{25}$.分析 该概型为几何概型,作出不等式组对应的平面区域,利用几何概型的概率公式求出相应的面积即可得到结论.
解答  解:∵[-3,2]内随机取一个整数m,在区间[-2,3]内随机取一个整数n,
解:∵[-3,2]内随机取一个整数m,在区间[-2,3]内随机取一个整数n,
∴以m为横坐标、n为纵坐标建立如图所示直角坐标系,
可得对应的点(m,n)在如图的正方形ABCD及其内部任意取,
正方形的面积为5×5=25,
∵x2+mx-$\frac{1}{4}$n2+$\frac{3}{4}$=0有两个不同的实数根,则△=m2-4(-$\frac{1}{4}$n2+$\frac{3}{4}$)=m2+n2-3>0,
即m2+n2>3,表示圆的外部的点,
则由几何概型的概率公式可得方程x2+mx-$\frac{1}{4}$n2+$\frac{3}{4}$=0有两个不同的实数根的概率P=1-$\frac{3π}{25}$,
故答案为:1-$\frac{3π}{25}$.
点评 本题主要考查概率的计算,根据几何概型的概率公式是解决本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.数列{an}是以a为首项,q为公比的等比数列,数列{bn}满足bn=1+a1+a2+…+an(n=1,2,…),数列{cn}满足cn=2+b1+b2+…+bn(n=1,2,…).若{cn}为等比数列,则a+q=( )
| A. | $\sqrt{2}$ | B. | 3 | C. | $\sqrt{5}$ | D. | 6 |
2.《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代具有很高的数学水平,其求法是“以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂,减上,余四约之,为实,一为从偶,开平方得积”,若把这段文字写成公式,即S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$,现有周长为10的△ABC满足sinA:sinB:sin:C=5:7:8,试用以上给出的公式求得△ABC的面积为( )
| A. | $\frac{5}{8}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 10$\sqrt{3}$ | D. | $\frac{35}{8}$ |
18.安排一张有5个独唱节目和3个合唱节目的节目单,要求任何2个合唱节目不相邻而且不排在第一个节目,那么不同的节目单有( )
| A. | 7200种 | B. | 1440种 | C. | 1200种 | D. | 2880种 |
 ,全集U=R。
,全集U=R。 时,求
时,求 和
和 ;
; ,求实数
,求实数 的取范围。
的取范围。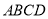 中,对角线
中,对角线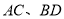 的交点为
的交点为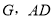 ⊥平面
⊥平面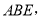
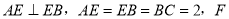 为
为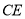 上的点,且
上的点,且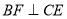 .
.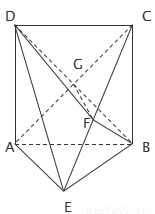
 ⊥平面
⊥平面 ;
; 的体积.
的体积.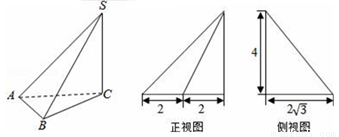
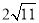 B.
B.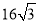 C.
C.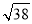 D.
D.