题目内容
5.已知动点P(x,y)在过点(-$\frac{3}{2}$,-2)且与圆M:(x-1)2+(y+2)2=5相切的两条直线和x-y+1=0所围成的区域内,则z=|x+2y-3|的最小值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | 1 | C. | $\sqrt{5}$ | D. | 5 |
分析 通过设过点(-$\frac{3}{2}$,-2)且与圆M相切的直线方程,利用直线与圆的位置关系可求出斜率,进而作出可行域,计算即得结论.
解答 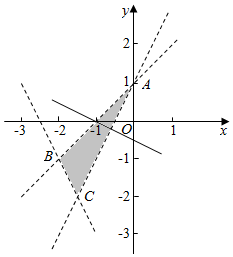 解:设过点(-$\frac{3}{2}$,-2)且与圆M相切的直线方程为:y+2=k(x+$\frac{3}{2}$),
解:设过点(-$\frac{3}{2}$,-2)且与圆M相切的直线方程为:y+2=k(x+$\frac{3}{2}$),
化简得:2kx-2y+3k-4=0,
则$\sqrt{5}$=$\frac{|2k+4+3k-4|}{\sqrt{4{k}^{2}+4}}$,解得:k=±2,
∴2x-y+1=0或2x+y+5=0,
∴约束条件表示的可行域如图,其中A(0,1),B(-2,-1),C(-$\frac{3}{2}$,-2),
所以z=|x+2y-3|的最小值为|0+2-3|=1,
故选:B.
点评 本题考查简单线性规划的应用,涉及直线与圆的位置关系、点到直线的距离公式等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列说法正确的是( )
| A. | P(B|A)<P(AB) | B. | P(B|A)=$\frac{P(B)}{P(A)}$是可能的 | ||
| C. | 0<P(B|A)<1 | D. | P(A|A)=0 |
15.已知函数f(x)=2x2+3,g(x)=a$\sqrt{{x}^{2}+1}$,若对于任意的x∈R,f(x)>g(x)恒成立,则实数a的取值范围是( )
| A. | (-∞,2$\sqrt{2}$) | B. | (-∞,2$\sqrt{2}$] | C. | (-∞,3) | D. | (-∞,3] |