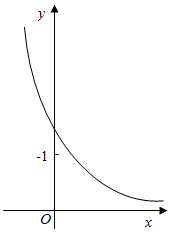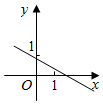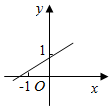题目内容
3.已知数列{an}满足a1=1,an+1=2n.(1)证明:数列{$\frac{{a}_{n}}{{2}^{n}}$}是等差数列,并求出{an}的通项公式;
(2)若cn=n•an,bn=$\frac{(n+2)•{2}^{n-1}}{{c}_{n}•{c}_{n+1}}$的前n项和为Sn,求证:$\frac{3}{4}$≤Sn<1.
分析 (1)通过a1=1、an+1=2n计算可知$\frac{{a}_{1}}{{2}^{1}}$=$\frac{1}{2}$、$\frac{{a}_{n+1}}{{2}^{n+1}}$=$\frac{1}{2}$,进而计算可得结论;
(2)通过(1)可知cn=n•2n-1,进而可知bn=$\frac{n+2}{n(n+1)}$•$\frac{1}{{2}^{n}}$,通过放缩、利用等比数列的求和公式计算即得结论.
解答 证明:(1)∵a1=1,an+1=2n,
∴$\frac{{a}_{1}}{{2}^{1}}$=$\frac{1}{2}$,$\frac{{a}_{n+1}}{{2}^{n+1}}$=$\frac{{2}^{n}}{{2}^{n+1}}$=$\frac{1}{2}$,
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}是首项为$\frac{1}{2}$、公差为0的等差数列,
∴$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}$,即数列{an}的通项公式an=2n-1;
(2)由(1)可知cn=n•an=n•2n-1,
∴bn=$\frac{(n+2)•{2}^{n-1}}{{c}_{n}•{c}_{n+1}}$=$\frac{(n+2)•{2}^{n-1}}{n(n+1)•{2}^{n-1}•{2}^{n}}$=$\frac{n+2}{n(n+1)}$•$\frac{1}{{2}^{n}}$,
∵$\frac{n+2}{n(n+1)}$=$\frac{1+\frac{2}{n}}{1+n}$∈(1,$\frac{3}{2}$],且$\frac{n+2}{n(n+1)}$<1,
∴Sn<$\frac{3}{4}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$
=$\frac{1}{4}$+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$
=$\frac{1}{4}$+$\frac{1}{2}$•$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$
<$\frac{1}{4}$+1-$\frac{1}{{2}^{2}}$
=1(n≥2),
又∵$\frac{3}{4}$≤Sn=S1,
∴$\frac{3}{4}$≤Sn<1.
点评 本题考查数列的通项及前n项和,考查裂项相消法,考查放缩法,注意解题方法的积累,属于中档题.

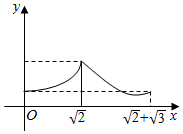
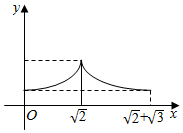
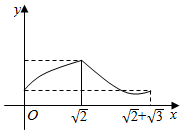
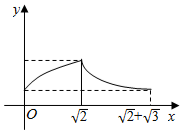
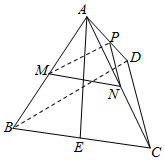 如图,在正三棱锥A-BCD中,M,N,E分别为AB,AC,BC边的中点,侧棱长为$\sqrt{2}$,且三条棱两两垂直,点P由A向E沿A→D→E运动,设点P运动的路程为x,△PMN的面积为y,则函数y=f(x)的图象大致是( )
如图,在正三棱锥A-BCD中,M,N,E分别为AB,AC,BC边的中点,侧棱长为$\sqrt{2}$,且三条棱两两垂直,点P由A向E沿A→D→E运动,设点P运动的路程为x,△PMN的面积为y,则函数y=f(x)的图象大致是( )