题目内容
已知点A,B分别是直线y=x和y=-x的动点(A,B在y轴的同侧),且△OAB的面积为![]() ,点P满足
,点P满足![]() .
.
(1)试求点P的轨迹C的方程;
(2)已知F![]() ,过O作直线l交轨迹C于两点M,N,若
,过O作直线l交轨迹C于两点M,N,若![]() ,试求△MFN的面积.
,试求△MFN的面积.
(3)理:已知F![]() ,矩形MFNE的两个顶点M,N均在曲线C上,试求矩形MFNE面积的最小值.
,矩形MFNE的两个顶点M,N均在曲线C上,试求矩形MFNE面积的最小值.
答案:
解析:
解析:
|
命题意图:本题抓住解析几何重点研究问题设问,熟悉巩固通性通法,典型几何条件如长、角等的代数转换方法,让学生理解解析几何的基本思想与策略.解析几何要把握好条件的等价翻译,理顺各量间的关系,计算准确,进而得出正确结论.取值范围、最值、存在性、定值等问题是高中数学的重点题型,要重视.最值问题一般要建立函数关系(求哪个量的最值,这个量一般是因变量,关键是找到主动变化的量,即自变量),并且指出函数的定义域(定义域往往和判别式有关).解析几何考最值要注意均值定理、导数和二次函数的运用. |

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目




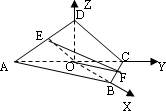

 是边长为
是边长为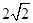 的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;
的正方形ABCD的中心,点E、F分别是AD、BC的中点,沿对角线AC把正方形ABCD折成直二面角D-AC-B;