题目内容
17.设各项均为正数的数列{an}的前n项和Sn满足$\frac{{S}_{n}}{{a}_{n}}$=$\frac{1}{3}$n+r.(1)若a1=2,求数列{an}的通项公式;
(2)在(1)的条件下,设bn=$\frac{1}{{a}_{2n-1}}$(n∈N*),数列{bn}的前n项和为Tn.求证:Tn≥$\frac{2n}{3n+1}$.
分析 (1)由$\frac{{S}_{n}}{{a}_{n}}$=$\frac{1}{3}$n+r,a1=2,可得r.于是Sn=$\frac{n+2}{3}{a}_{n}$,利用递推关系可得$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+1}{n-1}$,再利用“累乘求积”即可得出.
(2)bn=$\frac{1}{{a}_{2n-1}}$=$\frac{1}{(2n-1)(2n-1+1)}$≥$\frac{2}{(3n-2)(3n+1)}$=$\frac{2}{3}(\frac{1}{3n-2}-\frac{1}{3n+1})$.利用“裂项求和”即可得出.
解答 (1)解:∵$\frac{{S}_{n}}{{a}_{n}}$=$\frac{1}{3}$n+r,a1=2,
∴$\frac{{a}_{1}}{{a}_{1}}$=$\frac{1}{3}$+r=1,解得r=$\frac{2}{3}$.
∴Sn=$\frac{n+2}{3}{a}_{n}$,
当n≥2时,an=Sn-Sn-1=$\frac{n+2}{3}{a}_{n}$-$\frac{n+1}{3}{a}_{n-1}$,
化为:$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n+1}{n-1}$,
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$$•\frac{{a}_{n-1}}{{a}_{n-2}}$•$\frac{{a}_{n-2}}{{a}_{n-3}}$…$\frac{{a}_{3}}{{a}_{2}}$$•\frac{{a}_{2}}{{a}_{1}}$•a1=$\frac{n+1}{n-1}•\frac{n}{n-2}$$•\frac{n-1}{n-3}$•…•$\frac{4}{2}$$•\frac{3}{1}$•2=n(n+1),
当n=1时也成立,
∴an=n(n+1).
(2)证明:bn=$\frac{1}{{a}_{2n-1}}$=$\frac{1}{(2n-1)(2n-1+1)}$≥$\frac{2}{(3n-2)(3n+1)}$=$\frac{2}{3}(\frac{1}{3n-2}-\frac{1}{3n+1})$.
≥$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴数列{bn}的前n项和为Tn≥$\frac{2}{3}$$[(1-\frac{1}{4})+(\frac{1}{4}-\frac{1}{7})$+…+$(\frac{1}{3n-2}-\frac{1}{3n+1})]$
=$\frac{2}{3}$$(1-\frac{1}{3n+1})$=$\frac{2n}{3n+1}$.
∴Tn≥$\frac{2n}{3n+1}$.
点评 本题考查了递推关系、“累乘求积”、“裂项求和”、不等式的性质,考查了推理能力与计算能力,属于难题.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案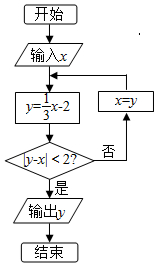 执行如图所示的程序框图,若输入x=9,则输出的y的值为( )
执行如图所示的程序框图,若输入x=9,则输出的y的值为( )| A. | -$\frac{23}{9}$ | B. | 1 | C. | $\frac{8}{9}$ | D. | -$\frac{5}{3}$ |
| A. | (-2,0)或(5,0) | B. | (8,9)或(10,0) | C. | (-2,0)或(8,0) | D. | (0,0)或(10,0) |
| A. | 3 | B. | $\frac{5}{2}$ | C. | 2 | D. | $\frac{3}{2}$ |