题目内容
6.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,其中|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是$\frac{3π}{4}$.分析 利用向量垂直的条件,结合向量数量积公式,即可求向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角
解答 解:设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,
∵|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$=${\overline{a}}^{2}$+$\overrightarrow{a}•\overrightarrow{b}$=${\overline{a}}^{2}$+|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=2+2$\sqrt{2}$cosθ=0,
解得cosθ=-$\frac{\sqrt{2}}{2}$,
∵0≤θ≤π,
∴θ=$\frac{3π}{4}$,
故答案为:$\frac{3π}{4}$
点评 本题考查向量的夹角的计算,考查向量数量积公式的运用,属于基础题.

练习册系列答案
相关题目
16.若存在两个正数x,y,使得等式${x^2}•{e^{\frac{y}{x}}}-2a{y^2}=0$成立,其中e为自然对数的底数,则实数a的取值范围是( )
| A. | $[{\frac{e^2}{8},+∞})$ | B. | $({0,\frac{e^3}{27}}]$ | C. | $[{\frac{e^3}{27},+∞})$ | D. | $({0,\frac{e^2}{8}}]$ |
17.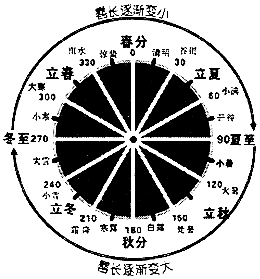 我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
 我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 四尺五寸 |
18.已知双曲线$\frac{{x}^{2}}{3}$-y2=1的右焦点是抛物线y2=2px(p>0)的焦点,直线y=kx+m与抛物线交于A,B两个不同的点,点M(2,2)是AB的中点,则△OAB(O为坐标原点)的面积是( )
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2$\sqrt{3}$ |