题目内容
20.已知实x,y数满足关系$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-y+4≥0}\\{y≥0}\end{array}}\right.$,则|x-2y+2|的最大值是5.分析 作出不等式组对应的平面区域,设u=2x+y-4,则z=|u|,利用u的几何意义,进行平移即可得到结论.
解答 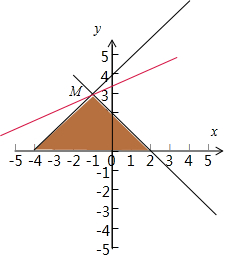 5 由条件可知:z=x-2y+2过点M(-1,3)时z=-5,|z|max=5,
5 由条件可知:z=x-2y+2过点M(-1,3)时z=-5,|z|max=5,
解:作出不等式组$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-y+4≥0}\\{y≥0}\end{array}}\right.$,对应的平面区域如图:由$\left\{\begin{array}{l}{x+y-2=0}\\{x-y+4=0}\end{array}\right.$解得M(-1,3),
由条件可知:z=x-2y+2过点M(-1,3)时z=-5,|z|max=5,
故答案为:5.
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.

练习册系列答案
相关题目
10.已知向量$\overrightarrow a=({1,2}),\overrightarrow b=({-2,m})$,若$\overrightarrow a∥\overrightarrow b$,则m=( )
| A. | -1 | B. | -4 | C. | 4 | D. | 1 |
11.钱大妈常说“便宜没好货”,她这句话的意思中:“好货”是“不便宜”的( )
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.已知定义在R上的偶函数f(x)满足f(x+1)=-f(x),且当x∈[-1,0]时,$f(x)={4^x}+\frac{3}{8}$,函数$g(x)={log_{\frac{1}{2}}}|{x+1}|-\frac{1}{8}$,则关于x的不等式f(x)<g(x)的解集为( )
| A. | (-2,-1)∪(-1,0) | B. | $({-\frac{7}{4},-1})∪({-1,-\frac{1}{4}})$ | C. | $({-\frac{5}{4},-1})∪({-1,-\frac{3}{4}})$ | D. | $({-\frac{3}{2},-1})∪({-1,-\frac{1}{2}})$ |
15.若$z=\frac{2-i}{2+i}$,则|z|=( )
| A. | $\frac{1}{5}$ | B. | 1 | C. | 5 | D. | 25 |
12.已知i是虚数单位,复数z满足(i-1)z=i,则z的虚部是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}i$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}$ |
10.为了解人们对于国家新颁布的“生育二孩放开”政策的热度,现在对某市年龄在35岁的人调查,随机选取年龄在35岁的100人进行调查,得到他们的情况为:在55名男性中,支持生二孩的有40人,不支持生二孩的有15人;在45名女性中,支持生二孩的有20人,不支持的有25人.
(Ⅰ)完成下面2×2列联表,并判断有多大的把握认为“支持生二孩与性别有关”?
附:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
(Ⅱ)在被调查的人员中,按分层抽样的方法从支持生二孩的人中抽取6人,再用简单随机抽样的方法从这6人中随机抽取2人,求这2人中恰好有1名男性的概率;
(Ⅲ)以上述样本数据估计总体,从年龄在35岁人中随机抽取3人,记这3人中支持生二孩且为男性的人数为X,求X的分布列和数学期望.
(Ⅰ)完成下面2×2列联表,并判断有多大的把握认为“支持生二孩与性别有关”?
| 支持生二孩 | 不支持生二孩 | 合计 | |
| 男性 | 40 | 15 | 55 |
| 女性 | 20 | 25 | 45 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(Ⅲ)以上述样本数据估计总体,从年龄在35岁人中随机抽取3人,记这3人中支持生二孩且为男性的人数为X,求X的分布列和数学期望.