题目内容
如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为α,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.
(1)求证:QQ′∥平面ABB′;
(2)当b=2a,且α=![]() 时,求异面直线AC与DB′所成的角;
时,求异面直线AC与DB′所成的角;
(3)当a>b,且AC⊥DB′时,求二面角α的余弦值(用a,b表示).
解:(1)证明:连结BB′,
∵Q,Q′分别是BD,B′D′的中点,
∴QQ′∥BB′.
而BB′![]() 平面ABB′,
平面ABB′,
∴QQ′∥平面ABB′.
(2)以A为原点,AB、AD分别为x轴.z轴建立空间直角坐标系,如图.

由条件可设A(0,0,0),B(a,0,0),C(a,0,b),D(0,0,b),
又∠BAB′=![]() ,AB′=a,∴B′(
,AB′=a,∴B′(![]() ,
,![]() ,0),C′(
,0),C′(![]() ,
,![]() ,b).
,b).![]() =(a,0,b),
=(a,0,b),![]() =(
=(![]() ,
,![]() ,-b),设异面直线AC与DB′所成角为θ,
,-b),设异面直线AC与DB′所成角为θ,
则cosθ= .
.
∵b2=2a2,∴cosθ=![]() .
.
故异面直线AC与DB′所成角为![]() .
.
(3)设B′(p,q,0),C′(p,q,b),∵AB′=a,∴p2+q2=a2.
∴![]() =(p,q,-b).又有
=(p,q,-b).又有![]() =(a,0,b),∵AC⊥DB′,∴
=(a,0,b),∵AC⊥DB′,∴![]() ·
·![]() =pa-b2=0,得pa=b2.
=pa-b2=0,得pa=b2.
设平面AB′C′D的法向量为n=(x,y,z),
∵n⊥![]() ,n⊥
,n⊥![]() ,而
,而![]() =(0,0,b),
=(0,0,b),![]() =(p,q,0).
=(p,q,0).
∴n=(![]() ,1,0),设平面ABCD的法向量为m,则m=(0,±1,0).
,1,0),设平面ABCD的法向量为m,则m=(0,±1,0).
∴cosα= =±
=±![]() =±
=±![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
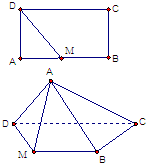 如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
