题目内容
如图, 矩形ABCD与矩形CDEF所在平面垂直, AB=4, AD=3, DE=2, 设∠CAF=α, ∠AFE=β, 则cosα:cosβ=___________
答案:5:4
解析:
提示:
解析:
|
解: 因为两平面互相垂直. 所以CF⊥平面CBAD.
所以CF⊥AC. cosα=
所以FE⊥AE. cosβ= 所以cosα:cosβ=AC:EF=5:4. |
提示:
|
发现∠AEF, ∠ACF为直角.
|

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目


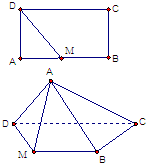 如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,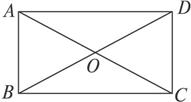
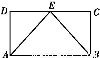
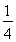
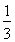
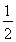

 BC=2 点E为BC的中点,点F在CD上。若
BC=2 点E为BC的中点,点F在CD上。若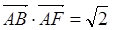 则
则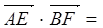 _____________。
_____________。
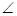 BCF=
BCF=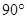 ,AD=
,AD=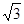 ,EF=2.
,EF=2.
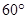 .
.