题目内容
如图,矩形ABCD中,AB=
(1)建立适当的平面直角坐标系,求椭圆M的方程;
(2)过椭圆M的中心作直线l与椭圆交于P,Q两点,设椭圆的右焦点为F2,当∠PF2Q=![]() 时,求△PF2Q的面积.
时,求△PF2Q的面积.
解:方程为![]() =1(a>b>0),
=1(a>b>0),

(1)依题意:![]() ,b=1,a2=b2+c2,
,b=1,a2=b2+c2,
∵椭圆M的离心率大于0.7,∴a2=4,b2=1.∴椭圆方程为![]() +y2=1.
+y2=1.
(2)∵直线l过原点与椭圆交于点P、Q,设椭圆M的左焦点为F1.
由对称性可知,四边形PF1QF2是平行四边形.∴△PF2Q的面积等于△PF1F2的面积.
∵∠PF2Q=![]() ,∴∠F1PF2=
,∴∠F1PF2=![]() .设|PF1|=r1,|PF2|=r2,则
.设|PF1|=r1,|PF2|=r2,则
 ∴r1r2=
∴r1r2=![]() .
.
∴![]() =
=![]() =
=![]() r1r2sin
r1r2sin![]() =
=![]() .
.

练习册系列答案
相关题目
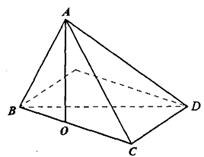 如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
如图,矩形ABCD中,AB=3,BC=4,沿对角线BD将
△ABD折起,使A点在平面BCD内的射影落在
BC边上,若二面角C—AB—D的平面有大小为
θ,则sinθ
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
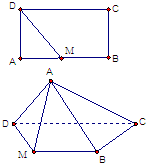 如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
如图矩形ABCD中,AB=2BC=2,M是AB中点,沿MD将AMD折起,
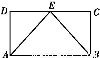
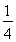
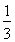
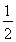

 BC=2 点E为BC的中点,点F在CD上。若
BC=2 点E为BC的中点,点F在CD上。若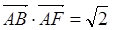 则
则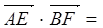 _____________。
_____________。