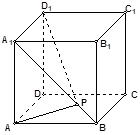题目内容
用 、
、 、
、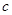 表示三条不同的直线,
表示三条不同的直线,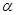 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ∥
∥ ,
, ∥
∥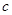 ,则
,则 ∥
∥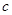 ; ②若
; ②若 ⊥
⊥ ,
, ⊥
⊥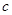 ,则
,则 ⊥
⊥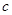 ;
;
③若 ∥
∥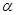 ,
, ∥
∥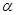 ,则
,则 ∥
∥ ; ④若
; ④若 ⊥
⊥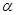 ,
, ⊥
⊥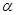 ,则
,则 ∥
∥ .
.
| A.①② | B.②③ | C.①④ | D.③④ |
C
解析试题分析:判断线与线、线与面、面与面之间的关系,可将线线、线面、面面平行(垂直)的性质互相转换,进行证明,也可将题目的中直线放在空间正方体内进行分析.解:根据平行直线的传递性可知①正确;在长方体模型中容易观察出②中a、c还可以平行或异面;③中a、b还可以相交;④是真命题,故答案应选:C
考点:空间线面位置关系
点评:在判断空间线面的关系,常常把他们放在空间几何体中来直观的分析,在判断线与面的平行与垂直关系时,正方体是最常用的空间模型,大家一定要熟练掌握这种方法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
设x、y、z是空间中不同的直线或平面,对下列四种情形:
①x、y、z均为直线;②x、y是直线,z是平面;③z是直线,x、y是平面;④x、y、z均为平面,其中使“x⊥z且y⊥z⇒x∥y”为真命题的是 ( )
| A.③④ | B.①③ |
| C.②③ | D.①② |
设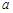 、
、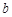 是两条不同的直线,
是两条不同的直线,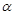 、
、 是两个不同的平面,是下列命题中正确的是( )
是两个不同的平面,是下列命题中正确的是( )
A.若 , ,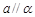 ,则 ,则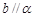 |
B.若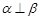 , ,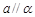 ,则 ,则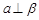 |
C.若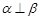 , ,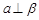 ,则 ,则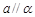 |
D.若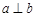 , , , , ,则 ,则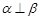 |
如图,在正方体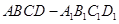 中,
中,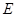 、
、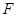 分别为棱
分别为棱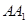 、
、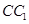 的中点,则在空间中与直线
的中点,则在空间中与直线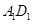 、
、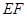 、CD都相交的直线有
、CD都相交的直线有
| A.1条 | B.2条 | C.3条 | D.无数条 |
设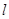 为直线,
为直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
 、
、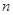 、
、 是三条不同的直线,
是三条不同的直线, 、
、 、
、 是三个不同的平面,给出以下命题:
是三个不同的平面,给出以下命题: ,则
,则 ; ②若
; ②若 ,则
,则 ;③若
;③若 ,
, ,则
,则 ;④若
;④若 ,
, ,则
,则 .
.



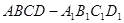 的面对角线
的面对角线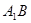 上存在一点
上存在一点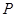 使得
使得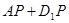 最短,则
最短,则