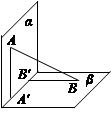题目内容
如图所示,正方体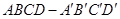 的棱长为1,O是平面
的棱长为1,O是平面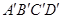 的中心,则O到平面
的中心,则O到平面 的距离是( )
的距离是( )
A.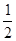 | B.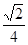 | C.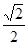 | D.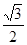 |
B
解析试题分析:因为O是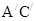 的中点,求O到平面
的中点,求O到平面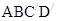 的距离,
的距离,
就是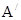 到平面
到平面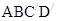 的距离的一半,
的距离的一半,
就是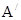 到
到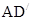 的距离的一半.
的距离的一半.
所以,连接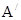 D与
D与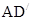 的交点为P,则
的交点为P,则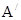 P的距离是O到平面
P的距离是O到平面 的距离的2倍,O到平面
的距离的2倍,O到平面 的距离
的距离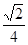 ,故选B。
,故选B。
考点:本题主要考查正方体的几何性质,距离的计算。
点评:基础题,正方体是立体几何中重要的几何体之一,其包含的平行关系、垂直关系等众多,是高考命题的重点内容之一。本题通过分析点O位置,明确O到平面 的距离与
的距离与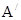 P的距离的关系是解题的关键。
P的距离的关系是解题的关键。

练习册系列答案
相关题目
如图,在正方体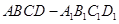 中,
中, 、
、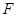 分别为棱
分别为棱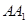 、
、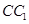 的中点,则在空间中与直线
的中点,则在空间中与直线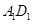 、
、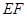 、CD都相交的直线有
、CD都相交的直线有
| A.1条 | B.2条 | C.3条 | D.无数条 |
如图,在长方体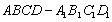 中,
中, ,
, ,则异面直线
,则异面直线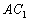 与
与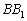 所成的角为 ( )
所成的角为 ( )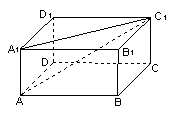
A.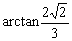 | B. | C.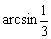 | D.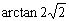 |
如图所示,正方体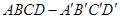 的棱长为1,O是平面
的棱长为1,O是平面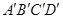 的中心,则O到平面
的中心,则O到平面 的距离是( )
的距离是( )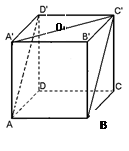
A. | B.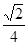 | C.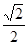 | D.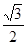 |
在正三棱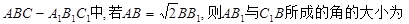 ( )
( )
A.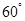 | B.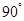 | C.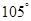 | D.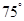 |
设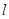 ,
,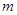 是两条不同的直线,
是两条不同的直线,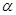 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若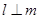 , ,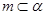 ,则 ,则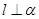 | B.若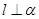 , ,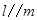 ,则 ,则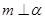 |
C.若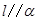 , ,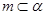 ,则 ,则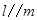 | D.若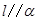 , ,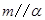 ,则 ,则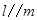 |
若a、b表示两条不同直线,α、β表示两个不同平面,则下列命题正确的是( )
A.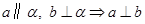 | B.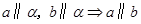 |
C.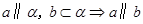 | D. |
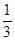
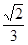
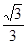
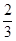
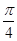 和
和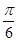 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )