题目内容
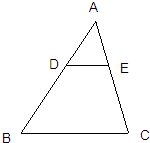（几何证明选讲选做题）如图，在△ABC中，已知DE∥BC，△ADE的面积是a2，梯形DBCE的面积是8a2，则
| AD |
| AB |
考点：相似三角形的性质
专题：计算题,解三角形
分析：根据DE∥BC得到△ADE∽△ABC，其相似比为
．再由△ADE的面积与△ABC的面积比为
，利用相似三角形的性质加以计算，可得的
值．
| AD |
| AB |
| 1 |
| 9 |
| AD |
| AB |
解答：
解：∵△ADE的面积是a2，梯形DBCE的面积是8a2，
∴△ABC的面积S=S△ADE+SDBCE=9a2．
∵在△ABC中，DE∥BC，∴△ADE∽△ABC，其相似比为
．
又∵
=
=
，∴（
）2=
，解得
=
．
故答案为：
∴△ABC的面积S=S△ADE+SDBCE=9a2．
∵在△ABC中，DE∥BC，∴△ADE∽△ABC，其相似比为
| AD |
| AB |
又∵
| S△ADE |
| S△ABC |
| a2 |
| 9a2 |
| 1 |
| 9 |
| AD |
| AB |
| 1 |
| 9 |
| AD |
| AB |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题给出△ABC中与一边平行的线段DE将△ABC分成梯形与小三角形的面积，求相似三角形的相似比．着重考查了平行线的性质、相似三角形的判定与性质等知识，属于基础题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
由圆x2+y2=1外一点P（2，1）引圆的切线，切线长为（ ）
A、
| ||
| B、2 | ||
| C、1 | ||
| D、4 |