题目内容
 已知一隧道的截面是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有0.5米的距离,现有一货车,车宽4米,车高2.5米.
已知一隧道的截面是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有0.5米的距离,现有一货车,车宽4米,车高2.5米.(1)若此隧道为单向通行,经测量隧道的跨度是10米,则应如何设计
隧道才能保证此货车正常通行?
(2)圆可以看作是长轴短轴相等的特殊椭圆,类比圆面积公式,请你推测椭圆
| x2 |
| a2 |
| y2 |
| b2 |
考点:椭圆的应用
专题:应用题,圆锥曲线的定义、性质与方程
分析:(1)以长轴所在直线为x轴,建立坐标系,求出椭圆方程,即可求出结论;
(2)利用
+
=1≥2
,即可得出结论.
(2)利用
| 16 |
| a2 |
| 9 |
| b2 |
|
解答:
 解:(1)以长轴所在直线为x轴,建立坐标系,设椭圆方程为
解:(1)以长轴所在直线为x轴,建立坐标系,设椭圆方程为
+
=1(a>b>0)则a=5,椭圆过(2,3),代入可得b=
,
∴隧道顶部离地面至少
米;
(2)椭圆的面积公式为πab,
∵椭圆过点(4,3),∴
+
=1≥2
,
当且仅当
=
=
时取等号,∴a=4
,b=3
,会使同等隧道长度下开凿的土方量最小.
 解:(1)以长轴所在直线为x轴,建立坐标系,设椭圆方程为
解:(1)以长轴所在直线为x轴,建立坐标系,设椭圆方程为| x2 |
| a2 |
| y2 |
| b2 |
5
| ||
| 7 |
∴隧道顶部离地面至少
5
| ||
| 7 |
(2)椭圆的面积公式为πab,
∵椭圆过点(4,3),∴
| 16 |
| a2 |
| 9 |
| b2 |
|
当且仅当
| 16 |
| a2 |
| 9 |
| b2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查椭圆方程,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
棱长都相等的正棱锥不可能是( )
| A、正三棱锥 | B、正四棱锥 |
| C、正五棱锥 | D、正六棱锥 |
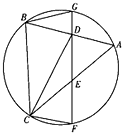 如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD.
如图,D,E分别是△ABC的边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,BG=BD. 如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明.
如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明. 某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,成绩如下表:
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,成绩如下表: