题目内容
8.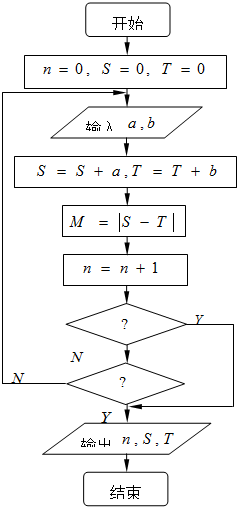 在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )
在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )| A. | M≥2,n>5 | B. | M=2,n=6 | C. | M>1,n≥6 | D. | M≥2,n<7 |
分析 由题意知M,n都是自然数,分析M,N的条件,即可得解.
解答 解:由题意知M,n都是自然数,所以对M的条件,只要是M≥2,M=2,M>1都行,对N的条件,只要满足N≥6,N=6,N>5可以,
故选:D.
点评 在2010-2014年的课标版全国卷中,算法初步的试题是每年必考的.2010年考查的是数列的裂项求和,2011年考查的是连续自然数的积,2012年考查的是求解一组数中的最大者,2013年考查的是分段函数的值域,2014年考查的是迭代运算,可见每年的算法试题都是以程序框图为命题背景,以算法与其它知识网络交汇点为命题载体,因此本题命制了算法的有关问题.本题中判断框中的条件可以有很多等价形式,如果判断不正确,容易进入误区.随着信息技术的发展,算法思想已经成为现代人应具备的一种数学素养,算法已经成为考生必须具备的新“双基”.该题的设计面向全体考生,让考生在解决具体数学问题的过程中理解程序框图的基本逻辑结构和语句,理解算法思想并能在实践中自觉应用.试题准确把握了算法教学的能力要求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某高中在一次数学考试中随机抽取100名学生的成绩,按成绩分组,得到的频率分布表如图所示
(Ⅰ)求出频率分布表中①、②位置相应的数据;
(Ⅱ)为了能选拔出最优秀的学生参加数学竞赛,学校决定在成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮测试,求第3、4、5组每组各抽取多少名学生进入第二轮测试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行抽查,求第4组至少有一名学生被抽查的概率?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [75,90] | 5 | 0.05 |
| 第2组 | (90,105] | ① | 0.35 |
| 第3组 | (105,120] | 30 | ② |
| 第4组 | (120,135] | 20 | 0.20 |
| 第5组 | (135,150] | 10 | 0.10 |
| 合计 | 100 | 1.00 | |
(Ⅱ)为了能选拔出最优秀的学生参加数学竞赛,学校决定在成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮测试,求第3、4、5组每组各抽取多少名学生进入第二轮测试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行抽查,求第4组至少有一名学生被抽查的概率?
20.某市践行“干部村村行”活动,现有3名干部可供选派,下乡到5个村蹲点指导工作,每个村至少有1名干部,每个干部至多住3个村,则不同的选派方案共有( )种.
| A. | 243 | B. | 210 | C. | 150 | D. | 125 |
18.f(x)=-2x2+mx-3在(-∞,3]上是增函数,则实数m的取值范围是( )
| A. | {1,2} | B. | [6,+∞) | C. | [12,+∞) | D. | (-∞,6] |
 某驾校为了保证学员科目二考试的通过率,要求学员在参加正式考试(下面简称正考)之前必须参加预备考试(下面简称预考),且在预考过程中评分标准得以细化,预考成绩合格者才能参加正考.现将10名学员的预考成绩绘制成茎叶图如图所示:
某驾校为了保证学员科目二考试的通过率,要求学员在参加正式考试(下面简称正考)之前必须参加预备考试(下面简称预考),且在预考过程中评分标准得以细化,预考成绩合格者才能参加正考.现将10名学员的预考成绩绘制成茎叶图如图所示: