题目内容
8.计算:log214-log27+log3(log2$\root{3}{2}$)+log23×log916.分析 根据对数的运算性质和换底公式计算即可.
解答 解:log214-log27+log3(log2$\root{3}{2}$)+log23×log916,
=log2$\frac{14}{7}$+log3($\frac{1}{3}$)+$\frac{lg3}{lg2}$•$\frac{lg16}{lg9}$,
=1-1+$\frac{lg3}{lg2}$•$\frac{4lg2}{2lg3}$,
=0+2,
=2.
点评 本题考查了对数的运算性质和换底公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.已知数列{an}是等差数列,a1+a7=-8,a2=2,则数列{an}的公差d等于( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
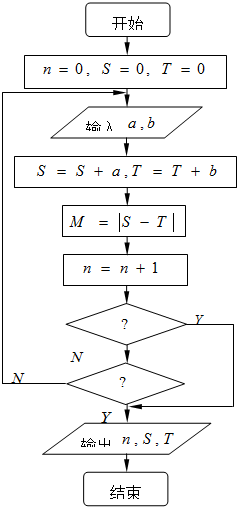 在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )
在某次中国象棋比赛中,组委会运用如图所示的程序框图统计比赛的总局数n及比赛双方的得分S、T.比赛约定每局胜者得1分,负者得0分,平局不作统计.如果一方获胜,输入a=1,b=0,另一方获胜,则输入a=0,b=1,比赛进行满6局或一方分数高于对方2分者即结束,则图中第一、第二两个判断框分别填写的条件错误的是( )