题目内容
已知一组曲线f(x)=alnx+bx+1,其中a∈{2,4,6,8},b∈{1,3,5,7},从这些曲线中任取两条,它们在点(1,f(1))处的切线恰好平行的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率,利用导数研究曲线上某点切线方程
专题:概率与统计
分析:由题意知,所有抛物线条数是4×4=16条,从16条中任取两条的方法数是C162=120,其中保证“它们在与直线x=1交点处的切线相互平行的”有14条,从而可求得它们在与直线x=1交点处的切线相互平行的概率.
解答:
解:a为2,4,6,8中任取一数,b为1,3,5,7中任取一数的曲线共16条,从这些曲线中任意抽取两条共C162=120种.
函数的f(x)的导数f′(x)=
+b,
则在x=1处的切线斜率k=f′(1)=a+b,
在与直线x=1交点处的切线的斜率为k=a+b因为切线相互平行,
则斜率相等,即a+b相等,
当a+b=5时,共(2,3),(4,1)两组,
当a+b=7时,共(2,5),(4,3),(6,1)三组,
当a+b=9时,共(2,7),(4,5),(6,3),(8,1)四组,
当a+b=11时,共(4,7),(6,5),(8,3),三组,
当a+b=13时,共(6,7),(8,5),两组,合计14组,
则对应的概率为
=
,
故选:B
函数的f(x)的导数f′(x)=
| a |
| x |
则在x=1处的切线斜率k=f′(1)=a+b,
在与直线x=1交点处的切线的斜率为k=a+b因为切线相互平行,
则斜率相等,即a+b相等,
当a+b=5时,共(2,3),(4,1)两组,
当a+b=7时,共(2,5),(4,3),(6,1)三组,
当a+b=9时,共(2,7),(4,5),(6,3),(8,1)四组,
当a+b=11时,共(4,7),(6,5),(8,3),三组,
当a+b=13时,共(6,7),(8,5),两组,合计14组,
则对应的概率为
| 14 |
| 120 |
| 7 |
| 60 |
故选:B
点评:本题主要考查了由导数的几何意义求解曲线的切线的斜率,两直线平行的条件的应用及古典概型两种概率问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
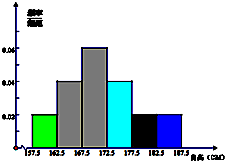 云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的平均身高为170.5cm.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],
云南省2014年全省高中男生身高统计调查数据显示:全省100000名男生的平均身高为170.5cm.现从我校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组[157.5,162.5],第二组[162.5,167.5],…,第6组[182.5,187.5],