题目内容
数列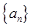 是首项
是首项 的等比数列,且
的等比数列,且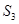 ,
,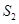 ,
, 成等差数列.
成等差数列.
(Ⅰ)求数列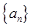 的通项公式;
的通项公式;
(Ⅱ)若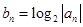 ,设
,设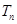 为数列
为数列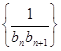 的前
的前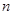 项和,若
项和,若 对一切
对一切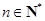 恒
恒
成立,求实数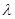 的最小值.
的最小值.
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)当 时,
时, ,不成等差数列 1分
,不成等差数列 1分
当 时,
时, ,∴
,∴ , 3分
, 3分
∴ ,∴
,∴ , 4分
, 4分
∴ . 5分
. 5分
(Ⅱ) , 6分
, 6分 , 7分
, 7分 , 8分
, 8分 ,∴
,∴ ,∴
,∴ , 10分
, 10分
又 ,∴
,∴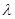 的最小值为
的最小值为 . 12分
. 12分
考点:等比数列通项及数列求和
点评:等比数列求和时需注意分公比 两种情况,一般数列求和常用的方法有分组求和法,裂项相消法,倒序相加法,错位相减法,本题利用的是裂项相消法,此法适用于通项公式为
两种情况,一般数列求和常用的方法有分组求和法,裂项相消法,倒序相加法,错位相减法,本题利用的是裂项相消法,此法适用于通项公式为 形式的数列
形式的数列

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 的各项均为正数,
的各项均为正数,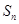 为其前
为其前 项和,对于任意的
项和,对于任意的 ,总有
,总有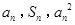 成等差数列.
成等差数列.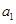 ;
;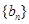 的前
的前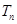 ,且
,且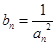 ,求证:对任意正整数
,求证:对任意正整数
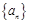 是等差数列,
是等差数列,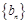 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且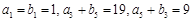
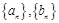 的通项公式;
的通项公式;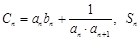 为数列
为数列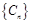 的前
的前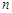 项和,求
项和,求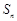 .
.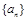 和公比为
和公比为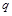
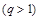 的等比数列
的等比数列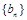 满足:
满足: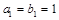 ,
,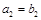 ,
,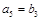 .
.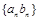 的前
的前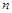 项和为
项和为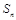 .
. 中,已知
中,已知 ,公比
,公比 ,等差数列
,等差数列 满足
满足 .
. ,求数列
,求数列 的前n项和
的前n项和 .
.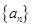 满足
满足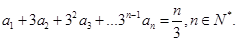
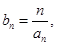 求数列
求数列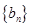 的前
的前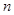 项和
项和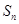 .
.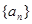 满足
满足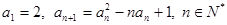 .
.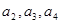 ,并由此猜想
,并由此猜想 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论;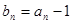 ,不等式
,不等式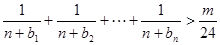 对一切
对一切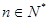 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。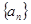 的前
的前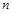 项和
项和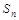 是二项式
是二项式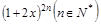 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.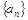 的通项公式;
的通项公式;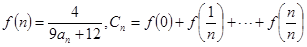 ,求
,求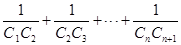 的值.
的值.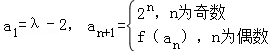 .
.