题目内容
设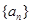 是首项为
是首项为 ,公差为
,公差为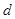 的等差数列(
的等差数列(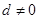 ),
),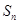 是前
是前 项和. 记
项和. 记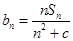 ,
,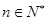 ,其中
,其中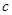 为实数.
为实数.
(1)若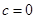 ,且
,且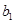 ,
,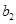 ,
,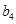 成等比数列,证明:
成等比数列,证明: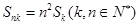 ;
;
(2)若 是等差数列,证明
是等差数列,证明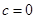 .
.
见解析
解析[证明](1)由题设,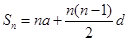 ,由
,由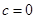 ,得
,得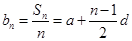 ,又
,又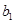 ,
,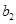 ,
,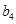 成等比数列,∴
成等比数列,∴ ,即
,即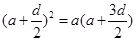 ,化简得
,化简得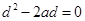 ,∵
,∵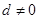 ,∴
,∴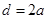 .
.
因此对于所有的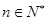
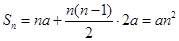 ,
,
从而对于所有的 ,
,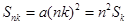 .
.
(2)设数列 的公差为
的公差为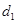 ,则
,则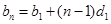 ,即
,即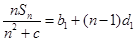 ,
,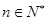 ,
,
代入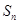 的表达式,整理得,对于所有的
的表达式,整理得,对于所有的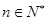 有
有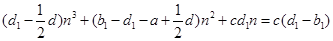 ,
,
令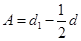 ,
,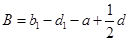 ,
,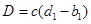 ,则对于所有的
,则对于所有的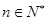 有
有 ,
,
在上式中取 ,
,
∴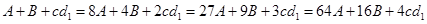 ,
,
从而有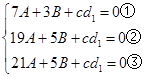 ,由②③得
,由②③得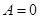 ,
,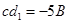 代入①得
代入①得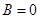 ,
,
从而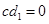 ,即
,即 ,
, ,
,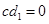 ,
,
若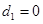 ,则由
,则由 得
得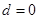 ,与题设矛盾,∴
,与题设矛盾,∴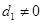 ,又
,又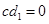 ,∴
,∴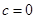 .
.
【考点定位】本小题主要考查等差、等比数列的定义、通项、求和等基础知识,考查分析转化以及推理论证能力.

练习册系列答案
相关题目
 的前
的前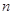 项和为
项和为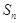 ,且满足
,且满足 ,
,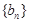 满足
满足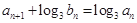 ,求数列
,求数列 .
. 的各项均为正数,
的各项均为正数,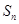 为其前
为其前 项和,对于任意的
项和,对于任意的 ,总有
,总有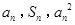 成等差数列.
成等差数列.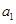 ;
;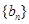 的前
的前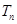 ,且
,且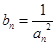 ,求证:对任意正整数
,求证:对任意正整数
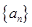 的前
的前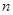 项和
项和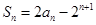 .
.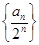 是等差数列;
是等差数列;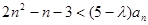 对
对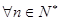 恒成立,求
恒成立,求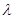 的取值范围.
的取值范围.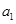 ,
,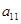 ,
,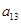 成等比数列.
成等比数列.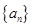 的通项公式;
的通项公式;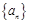 是等差数列,
是等差数列,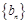 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且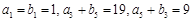
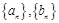 的通项公式;
的通项公式;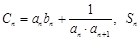 为数列
为数列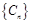 的前
的前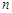 项和,求
项和,求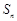 .
.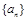 和公比为
和公比为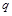
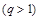 的等比数列
的等比数列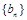 满足:
满足: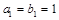 ,
,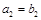 ,
,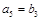 .
.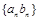 的前
的前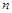 项和为
项和为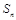 .
.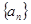 的前
的前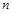 项和
项和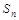 是二项式
是二项式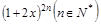 展开式中含
展开式中含 奇次幂的系数和.
奇次幂的系数和.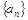 的通项公式;
的通项公式;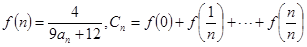 ,求
,求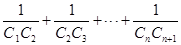 的值.
的值.