题目内容
定义在(-1,1)的函数f(x)满足:对任意x,y∈(-1,1)都有f(x)+f(y)=f(
),当x∈(-1,0)时有f(x)>0.
求证:f(
)+f(
)+…+f(
)>f(
).
| x+y |
| 1+xy |
求证:f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:先利用赋值法研究函数f(x)的性质,令x=y=0得,f(0)=0,再令y=-x,得f(-x)=-f(x),所以该函数是奇函数;再将
变成
,
则f(
)=f(
)+f(-
)=f(
)-f(
),则依此规律,然后利用列项法将左边化简,最后利用单调性解决问题.
| 1 |
| n2+3n+1 |
| ||||
1-
|
则f(
| ||||
1-
|
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
解答:
解:由已知令x=y=0代入f(x)+f(y)=f(
),得,f(0)=0;
同理,再令y=-x,得f(-x)=-f(x),所以该函数是奇函数,
再结合f(x)+f(y)=f(
),
∴f(
)=f(
)=f(
)-f(
),
∴原式左边=f(
)-f(
)+f(
)-f(
)+f(
)-f(
)+…+f(
)-f(
)
=f(
)-f(
),
∵当x∈(-1,0)时有f(x)>0,且f(x)是奇函数,
∴-f(
)=f(-
)>0,
∴f(
)-f(
)>f(
),
即f(
)+f(
)+…+f(
)>f(
).
| x+y |
| 1+xy |
同理,再令y=-x,得f(-x)=-f(x),所以该函数是奇函数,
再结合f(x)+f(y)=f(
| x+y |
| 1+xy |
∴f(
| 1 |
| n2+3n+1 |
| ||||
1-
|
| 1 |
| n+1 |
| 1 |
| n+2 |
∴原式左边=f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=f(
| 1 |
| 2 |
| 1 |
| n+2 |
∵当x∈(-1,0)时有f(x)>0,且f(x)是奇函数,
∴-f(
| 1 |
| n+2 |
| 1 |
| n+2 |
∴f(
| 1 |
| 2 |
| 1 |
| n+2 |
| 1 |
| 2 |
即f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| 2 |
点评:此题有一定难度.一般先利用赋值法求出f(0),f(1),f(-1)等等,然后判断函数的奇偶性,单调性等性质;同时本题联系到条件f(x)+f(y)=f(
),将左边拆项,错位相减进行化简,有一定的技巧性和难度,需要细细体会.
| x+y |
| 1+xy |

练习册系列答案
相关题目
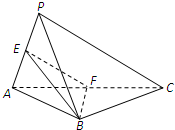 如图,在三棱锥P-ABC中,平面ABC⊥平面PAC,AB=BC,E,F分别是PA,AC的中点.求证:
如图,在三棱锥P-ABC中,平面ABC⊥平面PAC,AB=BC,E,F分别是PA,AC的中点.求证: