题目内容
如图,在长方体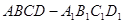 中,
中,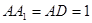 ,
,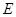 为
为 的中点,
的中点,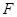 为
为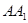 的中点.
的中点.
(I)求证: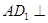 平面
平面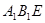 ;
;
(II)求证: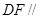 平面
平面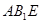 ;
;
(III)若二面角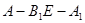 的大小为
的大小为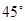 ,求
,求 的长.
的长.
(Ⅰ)详见解析;(Ⅱ)详见解析;(III)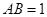 .
.
解析试题分析:(Ⅰ)证明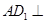 平面
平面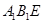 ,就是证明
,就是证明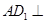 平面
平面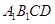 ,只需证明
,只需证明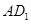 与平面
与平面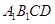 内的两条直线垂直,即可证明
内的两条直线垂直,即可证明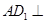 平面
平面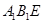 ;(Ⅱ)证明
;(Ⅱ)证明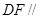 平面
平面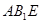 ,只需证明
,只需证明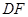 与平面
与平面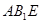 的一条直线平行,这里采用证明平行四边形的目的来证明
的一条直线平行,这里采用证明平行四边形的目的来证明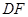 与平面
与平面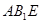 的一条直线平行;(III)借助空间向量法计算当
的一条直线平行;(III)借助空间向量法计算当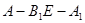 为
为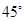 时
时 的长.
的长.
试题解析:(I)证明:在长方体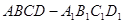 中,
中,
因为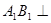 平面
平面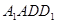 ,所以
,所以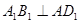 .
.
因为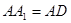 ,所以四边形
,所以四边形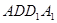 为正方形,因此
为正方形,因此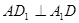 ,
,
又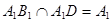 ,所以
,所以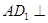 平面
平面 .
.
又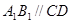 ,且
,且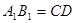 ,
,
所以四边形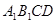 为平行四边形.
为平行四边形.
又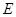 在
在 上,所以
上,所以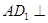 平面
平面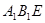 .
.
4分
(II)取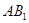 的中点为
的中点为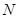 ,连接
,连接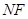 .
.
因为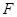 为
为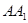 的中点,所以
的中点,所以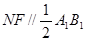 且
且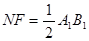 ,
,
因为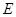 为
为 的中点,所以
的中点,所以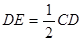 ,
,
而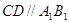 ,且
,且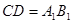 ,
,
所以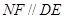 ,且
,且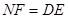 ,
,
因此四边形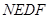 为平行四边形,
为平行四边形,
所以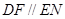 ,而
,而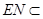 平面
平面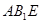 ,[来源:Z,xx,k.Com]
,[来源:Z,xx,k.Com]
所以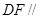 平面
平面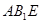 .
.
9分
(III)如图,以 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系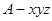 ,设
,设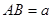 ,
,
则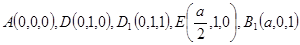 ,
,
故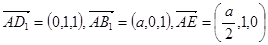 .
.
由(I)可知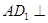 平面
平面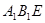 ,所以
,所以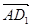 是平面
是平面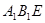 的一个法向量.
的一个法向量.
设平面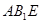 的一个法向量为
的一个法向量为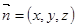 ,则
,则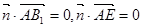 ,
,
所以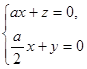
令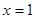 ,则
,则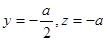 ,所以
,所以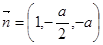 .
.
设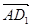 与
与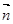 所成的角为
所成的角为
练习册系列答案
相关题目
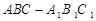 的底面是直角三角形,
的底面是直角三角形, 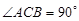 ,侧棱与底面所成角为
,侧棱与底面所成角为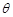 ,点
,点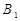 在底面上的射影
在底面上的射影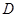 落在
落在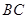 上.
上.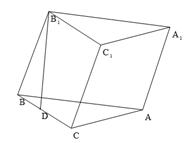
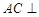 平面
平面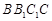 ;
;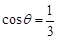 ,且当
,且当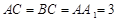 时,求二面角
时,求二面角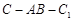 的大小.
的大小. 中,
中, 平面
平面 .
.
 的充分条件,并给予证明;
的充分条件,并给予证明; ,②
,② ;③
;③ 为锐角,求平面
为锐角,求平面 与平面
与平面 所成锐二面角
所成锐二面角 的取值范围.
的取值范围. ,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点
,将△AED、△CFD分别沿DE、DF折起,使A、C两点重合于点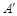 ,连结A¢B.
,连结A¢B.
 中,
中,
 底面
底面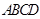 ,
, ,
, ,
, .
. 平面
平面 ;
;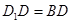 ,求四棱锥
,求四棱锥 的体积.
的体积.
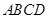 中,
中, 是
是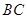 的中点,
的中点, ,
,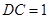 ,
,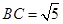 ,
,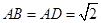 ,将左图沿直线
,将左图沿直线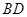 折起,使得二面角
折起,使得二面角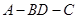 为
为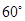 ,如右图.
,如右图.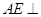 平面
平面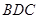 ;
; 与平面
与平面 所成角的余弦值.
所成角的余弦值.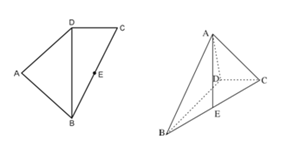
 的4个顶点都在球
的4个顶点都在球 的表面上,
的表面上, 为球
为球 为球面上一点,且
为球面上一点,且 平面
平面  ,点
,点 为
为 的中点.
的中点.  平面
平面 ;
; 到平面
到平面 的距离.
的距离.
 的边长为2,
的边长为2, 分别为边
分别为边 的中点,
的中点, 是线段
是线段 的中点,如图,把正方形沿
的中点,如图,把正方形沿 .
.
 取何值,
取何值, 与
与 不可能垂直;
不可能垂直; 的大小为
的大小为 ,当
,当 时,求
时,求 的值.
的值.
 的值.
的值.